好像没学过,最近读论文发现不太懂,于是简单补一些内容
NTP 协议
现代计算机系统依赖石英晶体振荡器来跟踪物理时间(UTC),这种硬件时钟通过主板电池供电确保断电后仍能持续运行。然而,石英钟存在固有的时钟漂移(clock drift)现象,其晶体振荡频率受温度、老化等因素影响,导致系统时间与真实时间逐渐产生偏差。两个独立计算机时钟的偏差值(clock skew)会随着时间累积而扩大,这种偏差在分布式系统中可能引发数据一致性问题、安全协议失效等严重后果。为解决这一问题,网络时间同步技术应运而生,其中最具代表性的协议是 网络时间协议(NTP)。
NTP协议的设计核心在于构建分层的时钟同步体系:
- Stratum 0: atomic clock or GPS receiver
- Stratum 1: synced directly with stratum 0 device
- Stratum 2: servers that sync with stratum 1, etc.
操作系统厂商普遍预置NTP客户端,通过轮询多个Stratum服务器获取时间样本,利用算法剔除异常值后取均值,从而在理想网络条件下将时钟偏差控制在毫秒级。
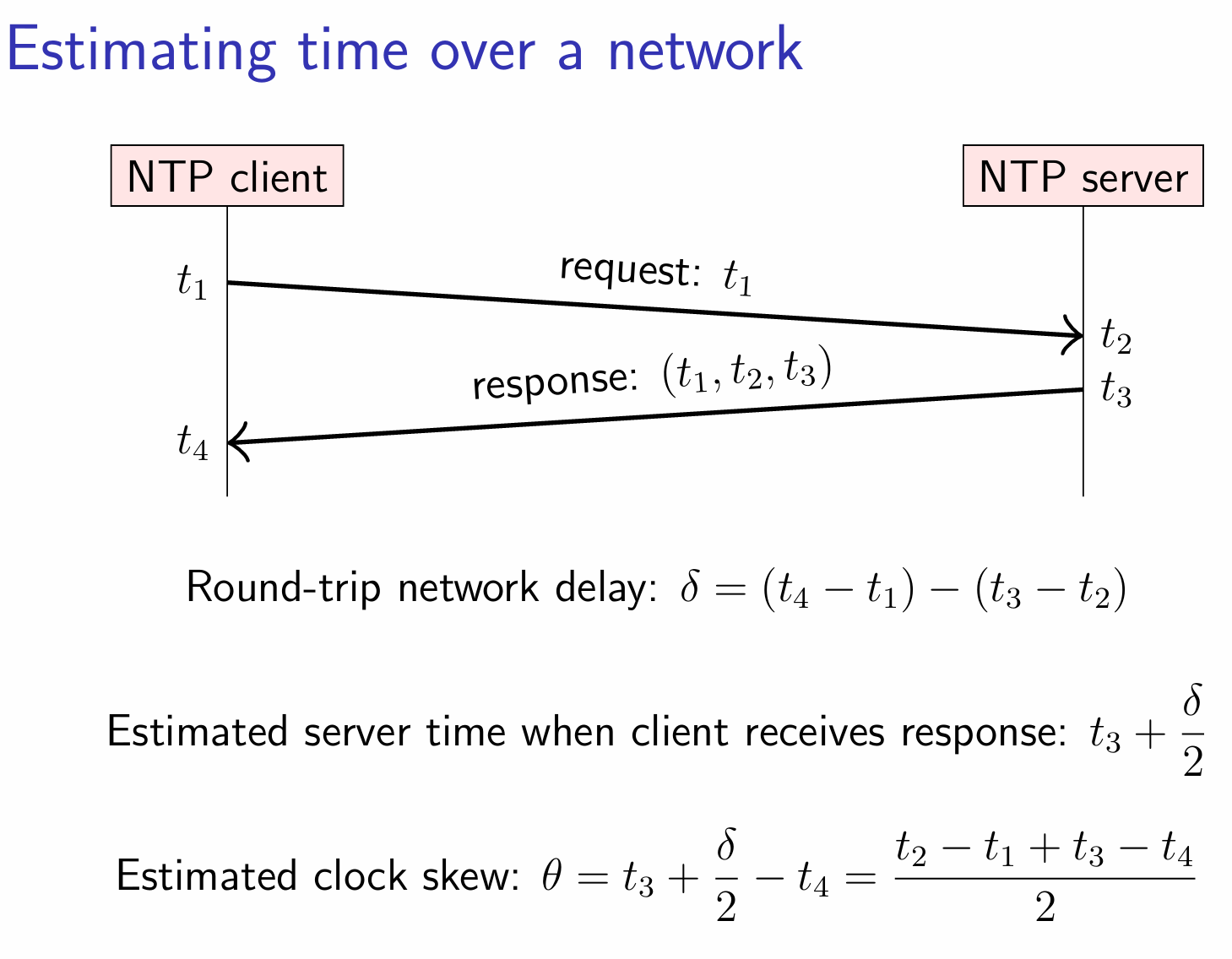
例如可以在 Python 中通过 ntplib 包来进行时间同步测试:
def ntp_request(server, port=123):
client = socket.socket(socket.AF_INET, socket.SOCK_DGRAM)
client.settimeout(2.0)
packet = b'\x1b' + 47 * b'\x00'
client.sendto(packet, (server, port))
response, _ = client.recvfrom(1024)
client.close()
return response运行可以得到
Server | Round-trip Delay | Clock Skew | Local Time (Adjusted)
-------------------------------------------------------
阿里云 | 0.011685 | -6.720525 | 2025-10-07 02:23:02.362
腾讯云 | 0.063014 | -6.721144 | 2025-10-07 02:23:02.442
腾讯云 | 0.061774 | -6.716030 | 2025-10-07 02:23:02.514
腾讯云 | 0.052554 | -6.717848 | 2025-10-07 02:23:02.574
腾讯云 | 0.059958 | -6.716593 | 2025-10-07 02:23:02.645
腾讯云 | 0.059004 | -6.716027 | 2025-10-07 02:23:02.714
苹果 | 0.068835 | -6.714274 | 2025-10-07 02:23:07.920
Google | 0.085312 | -6.716042 | 2025-10-07 02:23:08.008
Google | 0.083489 | -6.716909 | 2025-10-07 02:23:08.094
Google | 0.076374 | -6.717340 | 2025-10-07 02:23:08.174
Google | 0.088302 | -6.717644 | 2025-10-07 02:23:08.267时钟调整策略采用分级机制:当偏移量小于125毫秒时,通过slew the clock(±500ppm)在数分钟内逐步消除偏差;在125毫秒至1000秒范围内采用step the clock(直接设置时间),而超过1000秒的偏差则触发保护机制,需人工干预(panic)。这种设计既保证了日常同步的平滑性,又避免了大幅时间跳跃对应用程序的影响。但骤调操作可能导致时间回退现象,例如Java中使用 System.currentTimeMillis() 测量耗时时,若期间发生时钟骤调,可能出现负值结果。因此现代系统普遍引入单调时钟(monotonic clock),如 System.nanoTime(),其计时基准点随机(如系统启动时间),仅保证单调递增,不受NTP骤调影响,专用于精确测量时间间隔。
因果与 happens-before
在分布式系统中,事件的因果顺序是确保系统行为一致性的核心问题。以下面场景为例:用户A发送消息m1,用户B收到后回复m2,但由于网络重排序,用户C可能先收到m2再收到m1。这种看似“未来预知”的现象揭示了分布式系统中消息传递的固有挑战——网络延迟和乱序可能导致逻辑矛盾。更技术化的场景中,若m1是创建数据库对象的指令而m2是更新该对象的操作,处理顺序错误将导致m2因找不到目标对象而失败,进而破坏系统状态的一致性。
我们称事件 a 发生在事件 b 之前(记作 a happens before b , a \rightarrow b ),当且仅当满足以下任一条件:
- 事件 a 和事件 b 发生在同一节点上,且在该节点的本地执行顺序中, a 发生在 b 之前;
- 事件 a 是某条消息 m 的发送事件,而事件 b 是同一条消息 m 的接收事件(假设所发送的消息是唯一的);
- 存在一个事件 c ,使得 a \rightarrow c 且 c \rightarrow b 。
happens before 关系是一种偏序关系:可能存在既不满足 a \rightarrow b ,也不满足 b \rightarrow a 的情况。此时,称事件 a 与事件 b 是并发的(记作 a \parallel b )。

因果(Causality)的概念源自相对论:
- 当 a \rightarrow b 时, a 可能导致了 b 。
- 当 a \parallel b 时,那么 a 不可能导致 b 。
设 \prec 为事件集上的一个严格全序关系。 如果 (a \rightarrow b) \implies (a \prec b) ,则称 \prec 是一个因果序(causal order),或称: \prec = “与因果关系一致”。
时钟
逻辑时钟(Logical clocks)旨在捕捉因果依赖关系:
若 e_1 \rightarrow e_2 ,则必有 T(e_1) < T(e_2) 。
我们将讨论两种类型的逻辑时钟:
- Lamport 时钟
- 向量时钟(Vector clocks)
Lamport 时钟
on initialisation do
t := 0 #每个节点拥有自己的本地变量 t
end on
on any event occurring at the local node do
t := t + 1
end on
on request to send message m do
t := t + 1;
send (t, m) via the underlying network link
end on
on receiving (t′, m) via the underlying network link do
t := max(t, t′) + 1
deliver m to the application
end on- 每个节点维护一个计数器 t ,在每次本地事件 e 发生时递增。
- 令 L(e) 表示该事件发生后计数器 t 的值。
- 发送消息时,将当前的 t 值附加到消息中。
- 接收方收到消息后,若消息中的时间戳大于本地计数器,则将本地计数器更新为该时间戳,然后加 1。
Lamport clocks 的性质:
- 若 a \rightarrow b ,则 L(a) < L(b) 。
- 但 L(a) < L(b) 并不意味着 a \rightarrow b 。
- 可能存在 a \neq b 但 L(a) = L(b) 的情况。
设 N(e) 表示事件 e 所发生的节点。那么,二元组 (L(e), N(e)) 可唯一标识事件 e 。
利用 Lamport 时间戳定义一个全序关系 \prec :
(a \prec b) \iff \big(L(a) < L(b) \,\lor\, \big(L(a) = L(b) \,\land\, N(a) < N(b)\big)\big)
该全序关系是 causal 的: (a \rightarrow b) \implies (a \prec b)
向量时钟
给定 Lamport 时间戳 L(a) 和 L(b) ,即使 L(a) < L(b) ,我们仍无法判断是 a \rightarrow b 还是 a \parallel b 。
若要准确检测哪些事件是并发的,我们需要使用向量时钟:
- 假设系统中共有 n 个节点,记为 N = \langle N_1, N_2, \dots, N_n \rangle 。
- 事件 a 的向量时间戳为 V(a) = \langle t_1, t_2, \dots, t_n \rangle 。
- 其中 t_i 表示节点 N_i 所观察到的事件数量。
- 每个节点维护一个当前的向量时间戳 T 。
- 当节点 N_i 上发生一个事件时,将其向量中的第 i 个分量加 1。
- 发送消息时,将当前的向量时间戳附加到消息中。
- 接收方收到消息后,将其本地向量与消息中的向量逐分量取最大值进行合并,然后将自身分量加 1。
on initialisation at node N_i do
T := ⟨0, 0, ..., 0⟩ #节点 N_i 的本地变量
end on
on any event occurring at node N_i do
T[i] := T[i] + 1
end on
on request to send message m at node N_i do
T[i] := T[i] + 1;
send (T, m) via network
end on
on receiving (T′, m) at node N_i via the network do
for every j ∈ {1, ..., n} do
T[j] := max(T[j], T′[j])
end for
T[i] := T[i] + 1;
deliver m to the application
end on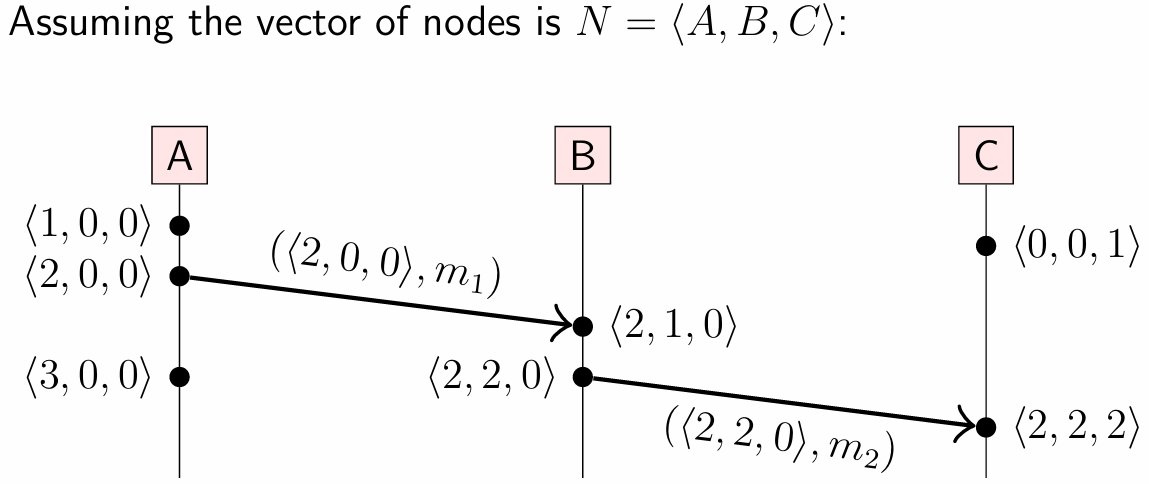
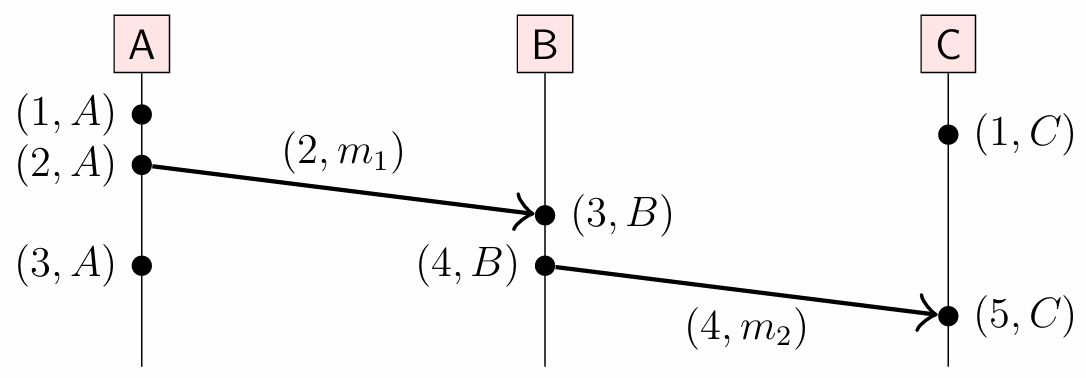
事件 e 的向量时间戳表示一个事件集合,即 e 本身及其所有因果前驱事件: {e} \cup {a \mid a \rightarrow e}
例如,向量 \langle 2, 2, 0 \rangle 表示:来自节点 A 的前两个事件、来自节点 B 的前两个事件,以及来自节点 C 的零个事件。
在包含 n 个节点的系统中,定义向量时间戳上的如下偏序关系:
- T = T' 当且仅当 对所有 i \in {1, \dots, n} ,有 T[i] = T'[i] 。
- T \leq T' 当且仅当 对所有 i \in {1, \dots, n} ,有 T[i] \leq T'[i] 。
- T < T^\prime 当且仅当 T \leq T^\prime 且 T \neq T^\prime 。
- T \parallel T' 当且仅当 T \nleq T' 且 T' \nleq T 。
该偏序关系具有如下语义: V(a) \leq V(b) \iff \big({a} \cup {e \mid e \rightarrow a}\big) \subseteq \big({b} \cup {e \mid e \rightarrow b}\big)
性质如下:
- V(a) < V(b) \iff a \rightarrow b
- V(a) = V(b) \iff a = b
- V(a) \parallel V(b) \iff a \parallel b