向量检索ANNS与维度灾难

本文系统介绍了k近邻(k-Nearest Neighbors, kNN)搜索算法，从精确方法到近似最近邻搜索(Approximate Nearest Neighbor Search, ANNS)技术，深入剖析了维度灾难(Curse of Dimensionality)的数学本质，并详解了局部敏感哈希(Locality Sensitive Hashing, LSH)、乘积量化(Product Quantization, PQ)及基于图的层次可导航小世界图(Hierarchical Navigable Small World, HNSW)等现代解决方案的原理与权衡。

kNN

给定一个包含 $n$ 个点的数据集 $P = {p_1, p_2, \dots, p_n}$ 和一个查询点 $q$ ，最近邻查询问题旨在找到 $P$ 中与 $q$ 距离最近的 $k$ 个点。距离通常通过某种度量函数 $d(p, q)$ 来衡量，例如欧几里得距离或余弦相似度。

朴素算法

对于每一个查询点 $q$ ，算法会计算 $q$ 与数据集中所有 $n$ 个点 $p_i$ 之间的距离 $d(q, p_i)$ 。然后，将这些距离按升序排序，并选择前 $k$ 个点作为结果。 $O(1)$ 预处理，若计算度量需要 $O(D)$ ，那么复杂度为 $O(n \cdot D + n \log k)=O(n \cdot D)$ ，这里通常 $D$ 比 $\log k$ 大。

$k$ -d Tree

构建：所有点中选择一个维度，找到该维度上的中位数作为分割点，将数据集分为两部分。然后对每个子集递归地在下一个维度上进行分割，直到每个叶节点包含足够少的点。复杂度 $O(n \cdot D \log n)$ 。

查询：从根开始根据查询点 $q$ 的坐标与当前节点的分割维度和分割值进入左右子树，找到一个初始的最近邻，然后在回溯的过程中计算当前节点到查询点 $q$ 的距离，并更新当前找到的 $k$ 个最近邻列表，根据到超平面的距离来决定是否进入其他子树查找。低维数据中复杂度为 $O(D \log n)$ ，在高维数据中，由于维度灾难，剪枝效率大幅下降，几乎所有子树都需要访问，查询时间会退化到接近 $O(n \cdot D)$ 。

Ball Tree

为了缓解维度灾难，相比 $k$ -d Tree 用立方体作为节点，Ball Tree 将点集包裹在超球体中来分割空间：每个节点代表一个包含其所有子节点和点的超球体。构建时递归地将超球体内的点集分为两个子集，并为每个子集创建更小的超球体，直到叶节点。

查询: 类似 $k$ -d Tree，根据查询点 $q$ 到超球体中心和边界的距离，来判断是否需要进入某个子树。比 $k$ -d Tree 在中高维度快很多，但是本质上仍受维度灾难影响，在高维下也接近 $O(n \cdot D)$ 。

维度灾难

$k$ -d树性能的退化现象是“维度灾难”（Curse of Dimensionality, CoD）的直接体现。维度灾难描述了当数据的特征维度 $D$ 增加时，许多在低维空间中成立的几何和统计特性开始失效，导致数据分布和异质性变得更加复杂和反直觉。这种现象不仅影响了数据索引结构，也造成了回归、分类或聚类模型的性能下降。

空间稀疏性

一个经典例子是比较 $D$ 维单位超立方体 $C_D = [-1, 1]^D$ 和其内切单位超球体 $B_D(1)$ （半径 $R=1$ ）的体积行为 5。超立方体的体积 $V_{\text{cube}} = 2^D$ 随维度呈指数级增长。相比之下， $D$ 维单位超球体的体积 $V_D$ 表达式为：

V_D = \frac{\pi^{D/2}}{\Gamma(D/2+1)}

其中 $\Gamma$ 是伽马函数 5。通过斯特林公式对 $\Gamma(D/2+1)$ 进行计算，可以得出数学结论：随着维度 $D \to \infty$ ，单位超球体的体积 $V_D$ 将非常迅速地趋近于零。这意味着在高维空间中，超立方体的绝大部分体积都被“掏空”了。如果数据点 $n$ 在超立方体内均匀分布，那么数据点密度 $n/V_{\text{cube}}$ 将以 $1/2^D$ 的速度急剧下降，造成极度的数据稀疏性。在高维空间中，任何两个数据点之间都会被巨大的空旷空间所分离。

体积集中化

高维几何体还有一个反直觉的特性，即体积的集中化：

超球体体积集中在表面 (Surface Concentration)：对于一个半径为 $R$ 的 $D$ 维超球体，其绝大部分体积集中在一个厚度与 $R/D$ 成比例的表面“壳”（rind/annulus）内。
超立方体体积集中在角落 (Corner Concentration)： $D$ 维单位超立方体的体积大多位于其 $2^D$ 个角落附近。

这种几何特性对 $k$ -d 树的构建产生了直接的负面影响。 $k$ -d 树采用轴对齐分割，本质上是在超立方体空间内进行划分。然而，由于高维数据的内在分布往往倾向于集中在一个低维流形上（Manifold Effect）或集中在超球体的表面，这种轴对齐划分无法有效地适应数据的真实几何结构。

距离集中化

在高维空间中，任意点 $q$ 到数据集中所有点 $p_i$ 的距离都趋向于聚集在平均距离附近。

对于一个点 $q$ ，我们关注其最近邻距离 $d_{NN}(q)$ 和最远邻距离 $d_{FN}(q)$ 。对于服从特定分布（如高斯分布或均匀分布）的高维数据集，可以证明这两个距离的比率趋近于 $1$ ：

\lim_{D \to \infty} \frac{d_{NN}(q)}{d_{FN}(q)} = 1

这种数学上的收敛意味着：

查询点 $q$ 看起来与数据集中的所有点几乎保持相同的距离。
距离度量的方差 $\text{Var}(d(p, q))$ 相比其期望 $\text E[d(p, q)]$ 变得微不足道。

$k$ -d 树的剪枝机制是基于分枝定界策略，其核心在于找到一个足够小的当前最佳距离 $\epsilon$ （即当前 $k$ 个最近邻中的最远距离）。剪枝条件要求待考察子树到查询点 $q$ 的最小距离 $d_{\min}$ 必须大于 $\epsilon$ ，才能安全地跳过该子树。

距离集中化对这个机制造成了致命打击：由于 $d_{NN} \approx d_{FN}$ ，当前最佳距离 $\epsilon$ 即使是最小的距离，也已经膨胀到一个较大的值，接近于所有点的平均距离 $d_{\text{avg}}$ 。这意味着几乎所有子区域到查询点 $q$ 的最小距离 $d_{\min}$ 都极有可能小于或等于这个已经膨胀的 $\epsilon$ 。因此，剪枝条件 $d_{\min} > \epsilon$ 几乎永远无法满足，导致算法必须继续探索几乎所有的分支。这时候 $k$ -d 树最坏情况时间复杂度 $T_{\text{worst}}$ 在计算几何中达到了经典的界限：

\lim_{D \to \infty} T_{\text{worst}} = \lim_{D \to \infty} O\left(D \cdot n^{1-\frac{1}{D}}\right)

在实际应用中，存在一个经验法则：为了保证 $k$ -d 树的查询效率优于线性搜索，数据集大小 $n$ 必须远大于 $2^D$ ( $n \gg 2^D$ )。

ANNS

因此，近似 kNN 算法应运而生。kANN 算法（也叫ANNS）不保证找到的 $k$ 个点是精确的最近邻，但它们与查询点足够“接近”，并且在可接受的精度损失下，能够显著提高查询速度和吞吐量。

Locality Sensitive Hashing, LSH

LSH 核心思想是设计一组哈希函数族，使得相似的点以高概率哈希到同一个桶中，而不相似的点以低概率哈希到同一个桶中。具体地，设 $\mathcal{X}$ 是一个数据空间， $d: \mathcal{X} \times \mathcal{X} \to \mathbb{R}$ 是一个距离度量。一个哈希函数族 $\mathcal{H}$ 被称为 $(r, c, p_1, p_2)$ -敏感的（其中 $r > 0$ , $c > 1$ , $p_1 > p_2$ ），如果对于任意两个点 $x, y \in \mathcal{X}$ ，满足：

如果 $d(x, y) \leq r$ ，则 $\Pr[h(x) = h(y)] \geq p_1$ 。
如果 $d(x, y) \geq c r$ ，则 $\Pr[h(x) = h(y)] \leq p_2$ 。

这里， $p_1$ 和 $p_2$ 是概率值，分别表示在“近”和“远”距离下哈希碰撞的概率。理想情况下， $p_1$ 接近 1， $p_2$ 接近 0，这样哈希函数能有效区分相似和不相似的点。

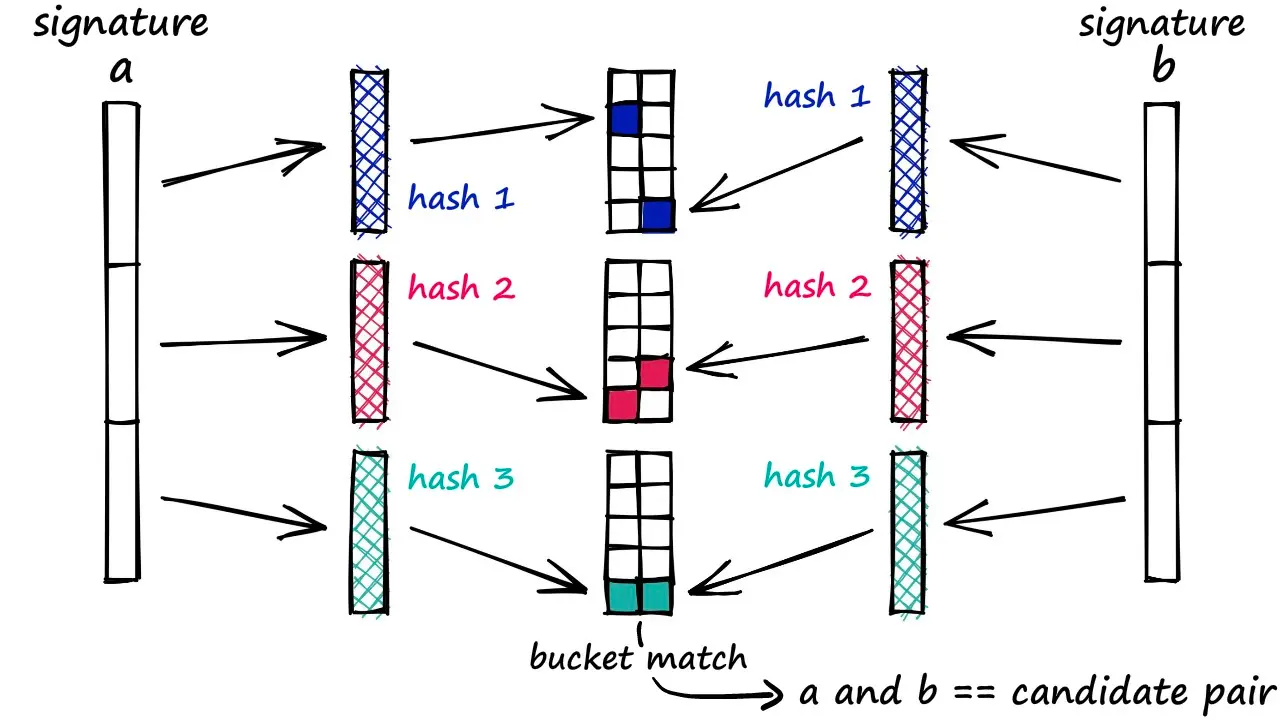
为了增强性能，LSH 通常使用多个哈希函数和多个哈希表，每个哈希表使用一个复合哈希函数 $g(x) = (h_1(x), h_2(x), \dots, h_k(x))$ ，其中 $h_i$ 是从 $\mathcal{H}$ 中独立随机选取的哈希函数。 $g(x)$ 将点映射到一个 $k$ -维哈希码，对应一个哈希桶。然后 LSH 使用 $L$ 个这样的复合哈希函数，构建 $L$ 个独立的哈希表。

构建：LSH 选择哈希函数族 $\mathcal{H}$ 和每个复合哈希函数的哈希函数数量 $k$ 和哈希表数量 $L$ 。对于每个哈希表 $j = 1, \dots, L$ ，生成一个复合哈希函数 $g_j(x) = (h_{j,1}(x), h_{j,2}(x), \dots, h_{j,k}(x))$ ，其中 $h_{j,i} \sim \mathcal{H}$ 。对于数据集中的每个点 $p_i$ ，计算 $g_j(p_i)$ 并将其插入到第 $j$ 个哈希表的对应桶中。复杂度为 $O(n \cdot L \cdot k \cdot D)$ ，其中 $n$ 是数据集大小， $k$ 通常和 $L$ 与 $n$ 相关。

查询：对于查询点 $q$ ，我们计算所有 $L$ 个复合哈希值 $g_j(q)$ 。对于每个 $j$ ，检索第 $j$ 个哈希表中与 $g_j(q)$ 对应的桶中的所有点加入候选集。对候选集中的点计算精确距离 $d(q, p)$ ，并返回最近邻或 top- $k$ 近邻。记 $B$ 为平均桶大小，复杂度为：计算哈希值 $O(L \cdot k \cdot D)$ 、检索桶 $O(L \cdot B)$ 、精确计算 $O(L \cdot B \cdot D)$ ，总时间为 $O(L \cdot B \cdot D)$ ，通常认为查询时间亚线性（ $O(n^\rho)$ ）。

常见距离度量对应的 LSH 哈希函数：

欧氏距离（L2距离）：基于 $p$ -稳定分布，将哈希函数定义为： $h_{\mathbf{a}, b}(x) = \left\lfloor \frac{\mathbf{a} \cdot x + b}{w} \right\rfloor$ ，其中： $\mathbf{a}$ 是一个随机向量，其分量来自标准正态分布 $N(0,1)$ ， $b$ 是一个在区间 $[0, w]$ 上均匀分布的随机偏移， $w$ 是桶宽参数，控制哈希桶的大小。

碰撞概率：对于两个点 $x$ 和 $y$ ，设 $d = |x - y|_2$ ，则：
$\Pr[h(x) = h(y)] = \int_0^w \frac{1}{d} f\left(\frac{t}{d}\right) \left(1 - \frac{t}{w}\right) \, dt$
其中 $f$ 是 $p$ -稳定分布的概率密度函数。

对于欧氏距离，这可以近似为 $\Pr[h(x) = h(y)] \approx 1 - 2\Phi(-w/d) - \frac{2}{\sqrt{2\pi} d/w} (1 - e^{-(d/w)^2 / 2})$ ，其中 $\Phi$ 是标准正态累积分布函数。参数 $w$ 通常通过实验调整， $k$ 和 $L$ 根据期望的召回率设置。
余弦相似度：基于随机超平面，将哈希函数定义为： $h_{\mathbf{a}}(x) = \text{sign}(\mathbf{a} \cdot x)$ ，其中 $\mathbf{a}$ 是一个随机向量，其分量来自标准正态分布 $N(0,1)$ 。

碰撞概率：对于两个点 $x$ 和 $y$ ，设 $\theta$ 是它们之间的夹角，则： $\Pr[h(x) = h(y)] = 1 - \frac{\theta}{\pi}$ 。因为 $\text{sign}(\mathbf{a} \cdot x) = \text{sign}(\mathbf{a} \cdot y)$ 当且仅当 $\mathbf{a}$ 与 $x$ 和 $y$ 的夹角相同侧。余弦相似度 $\sim \cos \theta$ ，所以碰撞概率与相似度正相关。

Product Quantization, PQ

PQ 是一种用于高维向量压缩和近似最近邻搜索的技术，其核心数学思想是将高维空间分解为多个低维子空间的笛卡尔积，并对每个子空间独立进行向量量化。这种分解允许我们以紧凑的方式表示向量，同时支持高效的近似距离计算。

2D chart showing our quantized 'PQ' vectors that have now been assigned to different Voronoi cells via IVF.

给定一个 $D$ 维向量 $\mathbf{x} \in \mathbb{R}^D$ ，PQ 首先将其划分为 $M$ 个互不相交的子向量，即 $\mathbf{x} = [\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_M]$ ，其中每个子向量 $\mathbf{x}_m$ 的维度为 $D/M$ （假设 $D$ 能被 $M$ 整除）。这种划分相当于将原始向量空间视为 $M$ 个子空间的直积，从而将高维量化问题分解为多个低维量化问题。对于每个子空间 $m$ ，我们使用 k-means 生成一个码本 $\mathcal{C}_m = {\mathbf{c}_{m,1}, \mathbf{c}_{m,2}, \dots, \mathbf{c}_{m,C}}$ ，其中 $\mathbf{c}_{m,i} \in \mathbb{R}^{D/M}$ 是码字， $C$ 是码本大小。码本的训练过程旨在最小化量化误差，即找到一组码字使得子向量到最近码字的平均距离最小化。

构建：对于数据集中的每个向量 $\mathbf{x}$ ，我们对其进行编码。对于每个子向量 $\mathbf{x}_m$ ，我们找到其最近的码字： $q_m(\mathbf{x}_m) = \arg\min_{\mathbf{c} \in \mathcal{C}_m} |\mathbf{x}_m - \mathbf{c}|$ ，并记录对应的索引 $i_m(\mathbf{x}) = \arg\min_{i=1,\dots,C} |\mathbf{x}_m - \mathbf{c}_{m,i}|$ 。最终，整个向量 $\mathbf{x}$ 被量化为 $q(\mathbf{x}) = [q_1(\mathbf{x}_1), q_2(\mathbf{x}_2), \dots, q_M(\mathbf{x}_M)]$ ，其存储表示是一个由 $M$ 个整数组成的元组 $(i_1, i_2, \dots, i_M)$ ，总存储空间为 $M \cdot \log_2 C$ 位。例如，当 $M=8$ 和 $C=256$ 时，每个向量仅需 64 位，相比原始浮点表示（如 128 维需 512 字节）极大地压缩了存储。复杂度主要开销来自 k-means 聚类 $O(K \cdot D \cdot n \cdot T)$ 和 PQ 编码 $O(n \cdot D \cdot C)$ 。

查询：给定一个查询向量 $\mathbf{q}$ ，我们需要快速计算它与数据库中压缩向量的近似距离。PQ 支持两种主要距离计算方式：非对称距离计算 (ADC) 和对称距离计算 (SDC)：

在 ADC 中，我们首先将 $\mathbf{q}$ 同样划分为 $M$ 个子向量 $\mathbf{q}_m$ 。然后，对于每个子空间 $m$ ，我们预先计算查询子向量与所有码字的距离，形成距离表 $\text{table}_m[i] = d(\mathbf{q}_m, \mathbf{c}_{m,i})$ ，其中 $d(\cdot,\cdot)$ 是距离度量。对于数据库中的每个压缩向量 $\mathbf{x}$ ，其近似距离通过查表求和得到： $\hat{d}(\mathbf{q}, \mathbf{x}) = \sum_{m=1}^M \text{table}_m[i_m(\mathbf{x})]$ 。
SDC 要求查询向量也被量化，即计算 $d(\mathbf{q}, \mathbf{x}) \approx \sum_{m=1}^M d(\mathbf{c}_{m,j_m(\mathbf{q})}, \mathbf{c}_{m,i_m(\mathbf{x})})$ ，其中 $j_m(\mathbf{q})$ 是 $\mathbf{q}$ 的量化索引。但由于查询向量的量化引入额外误差，SDC 的精度通常低于 ADC。

空间复杂度方面，原始数据存储为 $O(n \cdot D)$ ，而 PQ 压缩后仅需 $O(n \cdot M \cdot \log_2 C)$ 位用于存储编码，加上码本存储 $O(M \cdot C \cdot \frac{D}{M}) = O(C \cdot D)$ 。这使得 PQ 非常适用于大规模数据集。

PQ 是一种有损压缩方法，其核心误差源于量化过程。量化误差可以定义为 $\mathcal{E} = \mathbb{E}[|\mathbf{x} - q(\mathbf{x})|^2]$ ，即原始向量与量化向量之间的均方误差。对于子向量维度 $D/M$ ，量化误差满足 $\mathcal{E} \geq M \cdot C^{-2/(D/M)} \cdot \sigma^2$ ，其中 $\sigma^2$ 是子向量的方差。这表明，为了减少误差，我们可以增加码本大小 $C$ 或子空间数量 $M$ ，但这会增加存储和计算成本。

倒排文件索引 IVF

为了进一步提升搜索效率，PQ 常与倒排文件索引结合，形成 IVF-PQ 框架。IVF 首先使用 k-means 将整个数据集聚类成 $K$ 个簇，每个簇对应一个质心 $\mathbf{r}_k$ 和一个 Voronoi 胞腔 $V_k$ 。在构建索引时，每个数据点被分配到最近质心的簇中，并在簇内使用 PQ 进行压缩。

在查询时，对于查询向量 $\mathbf{q}$ ，我们首先找到 $w$ 个最近质心（即 $w$ 个最近簇），然后只在这些簇内进行搜索。距离计算结合了粗搜索和细搜索：首先计算 $\mathbf{q}$ 与质心的距离以确定候选簇，然后在候选簇内使用 PQ-ADC 计算近似距离。这种方法将搜索范围从整个数据集缩小到局部区域，显著减少了计算量。数学上，搜索召回率取决于 $P(\mathbf{x}^* \in \bigcup_{k \in \mathcal{N}_w(\mathbf{q})} V_k)$ ，即真实近邻落在候选簇内的概率。

基于图的方法

这类方法构建一个图，其中数据点是节点，边连接“相似”或“邻近”的点。搜索过程通过遍历图来找到查询点的近似最近邻。搜索算法通常直接使用贪心搜索，而建图则非常关键。

贪心搜索

维护候选列表 $L$ 和已访问集合 $V$ 。

从随机的/中心点作为起始点 $s$ ，每次从 $L \setminus V$ （未扩展的候选点）中选择距离查询点 $q$ 最近的点 $p^* = \arg\min_{p \in L \setminus V} d(q, p)$ 。选择 $p^*$ 后，算法将其所有出边邻居 $N(p^*)$ 添加到候选列表 $L$ 中，并将 $p^*$ 标记为已访问（加入 $V$ ）。这个过程不断重复，直到满足停止条件：可能达到最大迭代次数、 $L \setminus V$ 为空、或者候选列表大小达到预设阈值 $L_{max}$ 。最终从候选列表 $L$ 中返回 $k$ 个距离 $q$ 最近的点作为近似最近邻。

贪心搜索的时间复杂度高度依赖于图的结构质量。在一个良好构造的图中，搜索路径长度通常为 $O(\log n)$ 或 $O(\log^2 n)$ ，其中 $n$ 是数据集大小。这使得查询时间远低于线性扫描的 $O(n \cdot D)$ 。图的质量衡量标准包括图的直径和平均出度，这些因素共同决定了搜索效率。通常我们认为建出来的图应该具有下面性质：

稀疏性 Sparsity：图的边数通常远小于 $O(n^2)$ 。每个节点只连接少数邻居（平均度数 $R$ 通常是一个常数或一个小常数），以控制索引大小和查询时的距离计算量。
连通性 Connectivity：图必须足够连通，以确保从任意起始点都能找到通往查询目标区域的路径。
小世界特性 Small-World Property：理想的图应具有较小的直径，即任意两点之间的最短路径（跳数）很短。这对于减少磁盘 I/O 或内存访问次数至关重要。
可导航性 Navigability：图应该支持贪心搜索。这意味着在每一步，沿着图的边总能找到一个比当前点更接近查询点的邻居，或者至少能引导搜索走向正确的方向。这通常通过连接局部邻居（保证局部收敛）和长距离邻居（保证全局收敛和减小直径）来实现。
剪枝 Pruning：为了控制每个节点的度数并选择最有价值的邻居，构建算法通常会使用某种形式的剪枝策略。这有助于去除冗余边，同时保留对搜索至关重要的边。

Hierarchical Navigable Small World, HNSW

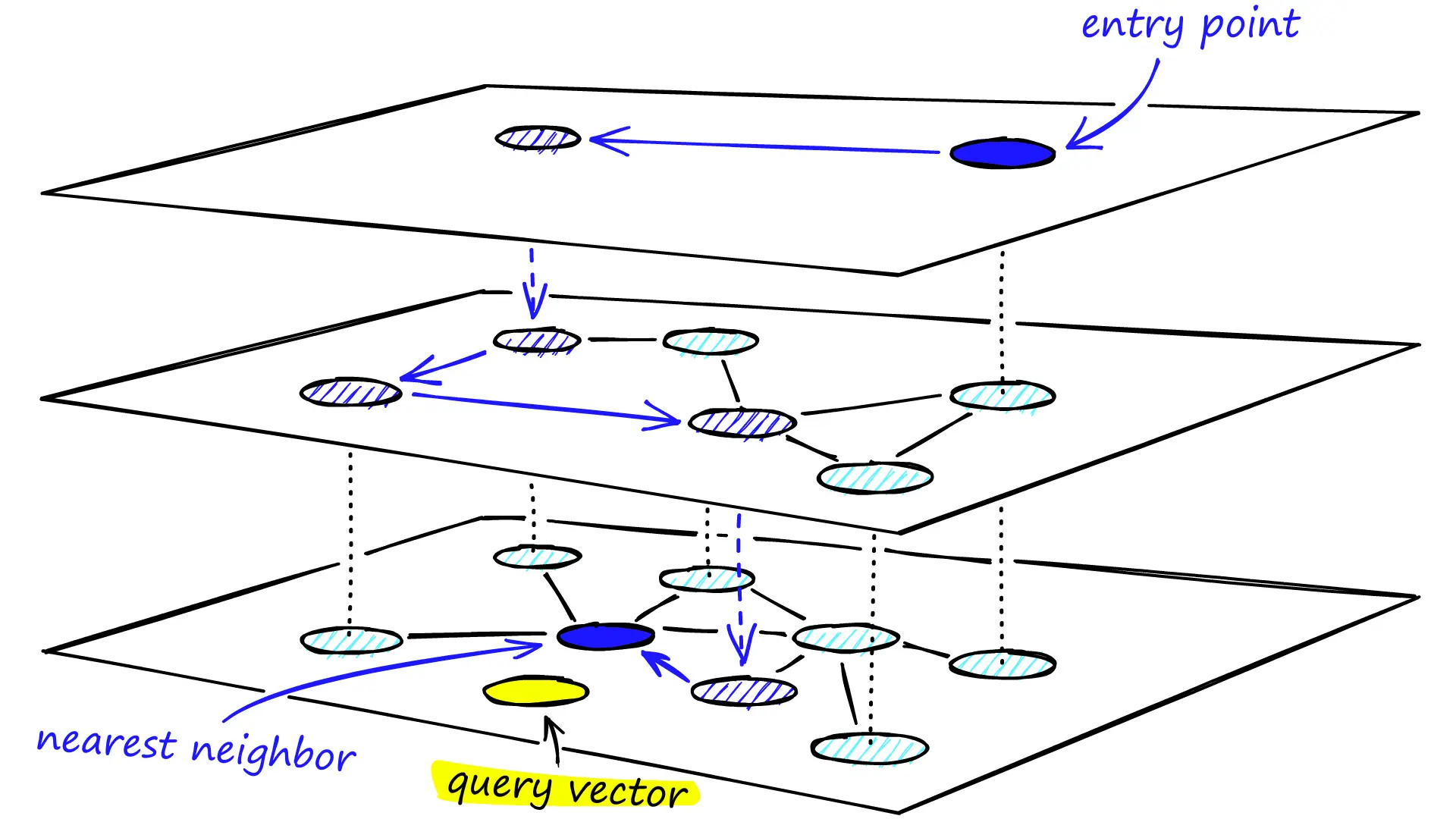
HNSW 从概率跳表中得到灵感，核心思想是构建一个多层图结构，模仿“小世界网络”的特性，即大多数节点之间通过少数几跳即可到达。

具体地，HNSW 由 $L_{max}$ 层组成，其中第 $0$ 层包含所有数据集点，而更高层包含较少的点，作为“高速公路”连接远距离点。每一层 $l$ 都是一个单独的图 $G_l = (P_l, E_l)$ ，其中 $P_l \subseteq P_{l-1}$ 。通常，一个点在层 $l$ 的邻居集合是它在层 $l-1$ 邻居集合的子集，但连接的“范围”更广。

构建过程：

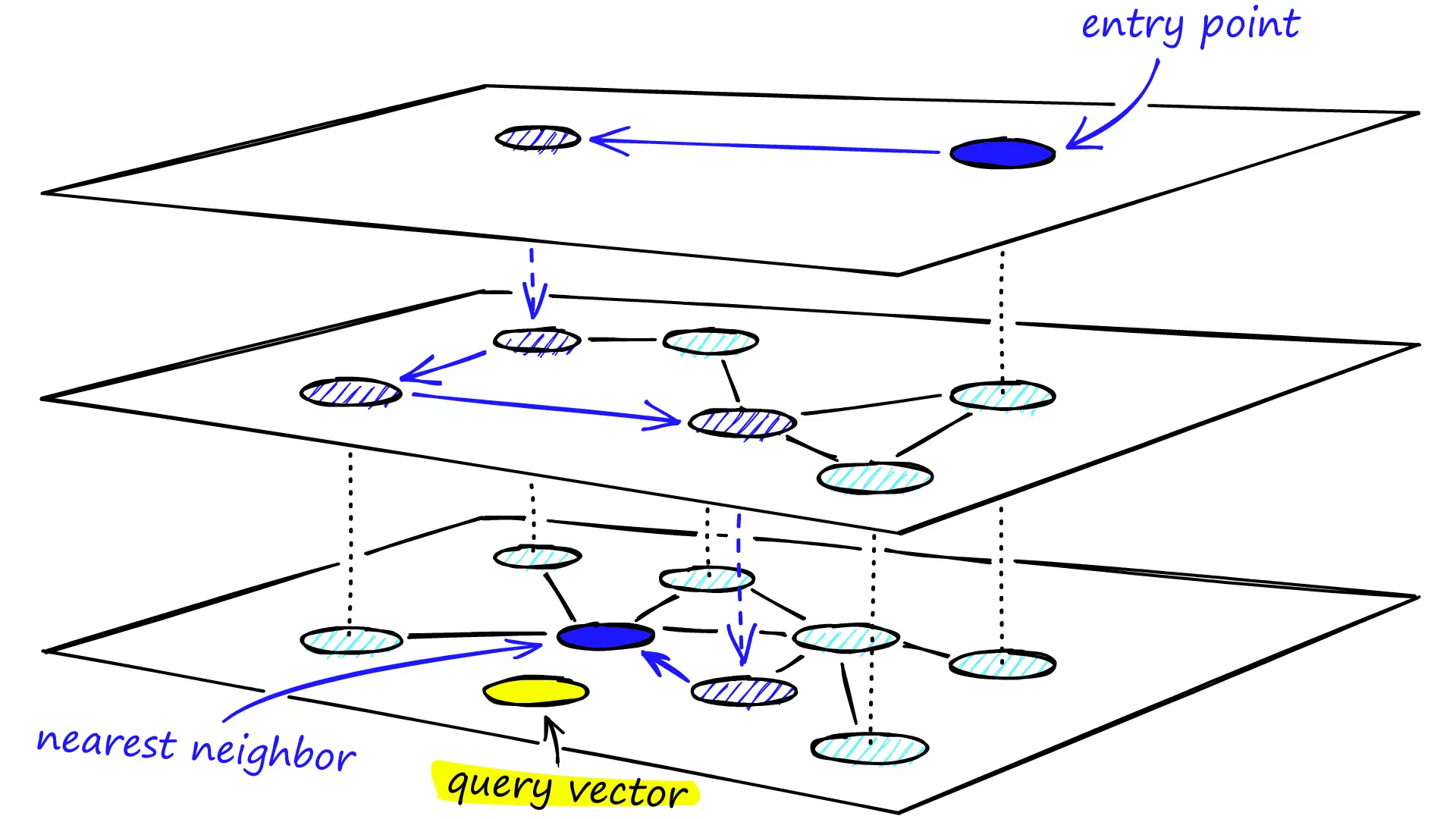
当插入一个新点 $p_{new}$ 时，首先通过随机过程（通常是指数分布，例如 $\min(-\ln(rand()), L)$ ）为其分配一个最高层 $l_{max}$ 。从最高层 $L_{max}$ 开始，在当前层 $l$ 通过贪心搜索查找查询点 $p_{new}$ 的 $efC$ 个近似最近邻。这里的 $efC$ 是一个构建参数，表示在构建时用于探索的候选列表大小。
接下来在当前层 $l$ 找到 $efC$ 个最近邻后，将这些邻居作为下一层的入口点，并选择 $M$ 个点与 $p_{new}$ 连接，重复步骤，逐层向下，直到最低层 $l=0$ 。

连接和剪枝 Pruning：使用一种启发式剪枝策略来选择这 $M$ 个邻居。通常，它会选择 $M$ 个离 $p_{new}$ 最近的邻居，并确保这些邻居能提供良好的“扩展”能力，避免连接到被其他已连接邻居“遮蔽”的点。具体来说，它会选择与 $p_{new}$ 距离最近的 $M$ 个点，并倾向于选择那些距离其他已连接邻居更远的点，以保证多样性。同时对每个邻居 $p_j$ ，如果 $p_j$ 的度数超过 $M_{max}$ ，则需要对 $p_j$ 的邻居集合进行剪枝，以保持度数限制。