本文通过线段树来高效解决并发分析中动态维护偏序关系的难题。传统方法如向量时钟在处理非流式更新时，成本高昂（ \mathcal O(nk) ）且不支持高效删除。本文为每对线程链维护一个专门的数据结构，查询任意事件间的可达性被转化为一个高效的区间查询操作。

Key findings: 在具有少量链的 DAG 上，动态可达性问题可以被高效地归约为另一个基础问题——动态后缀最小值问题。

背景

动态分析是分析和测试并发程序的常用方法。这类技术通过观察程序执行轨迹 \sigma ，并分析其中事件的依赖关系，以推断是否存在并发错误。核心在于维护一个表示这些事件依赖关系的偏序 P 。传统上，Vector Clocks (VCs) 是处理此类任务的标准数据结构。然而，VCs 在非流式（non-streaming）分析中效率低下，插入（和传播）每个新的偏序关系需要 \mathcal O(nk) 时间，其中 n 是轨迹的事件总数， k 是线程数。此外，VCs 无法高效处理现有偏序关系的删除操作，通常需要 \mathcal O(n^2) 时间重新计算。

CSSTs 概述

CSSTs 核心是为解决后缀最小值问题而设计的稀疏线段树（Sparse Segment Tree, SST）。设计利用了并发轨迹的两个关键特性：

1. 并发轨迹通常由少量线程 k 组成。
2. 偏序 P 通常包含 k 个全序链（或者数量与 k 成比例）。 在并发程序分析中， k 通常远小于 n 。

CSSTs 的主要目标是在此背景下，实现插入、删除和查询偏序关系操作的 \log 时间复杂度。具体地，CSSTs 进行了两项关键优化：

1. Sparse Tree Representation: 仅为存在依赖关系的区间创建节点，使树的高度和操作复杂度同时受限于 \log n 和跨链密度 d ，即 \mathcal O(\min(\log n,d)) 。（看着很像动态开点？）
2. Minima Indexing: 节点额外记录最小值的位置，允许后缀查询提前终止遍历，加速查询。

基于 SST，CSSTs 提供了两种工作模式：

1. Fully Dynamic：支持边的插入与删除。每个 SST 仅存储直接依赖，查询时通过一个 \mathcal O(k^3) 的不动点计算来推导传递关系，更新开销低至 \mathcal O(\log n) 级别。
2. Incremental：仅支持边插入。每个 SST 维护完整的传递可达性，更新时以 \mathcal O(k^2) 的代价传播依赖，将查询简化为一次 \mathcal O(\min(\log n,d)) 的 SST 查询。

2 条链的做法

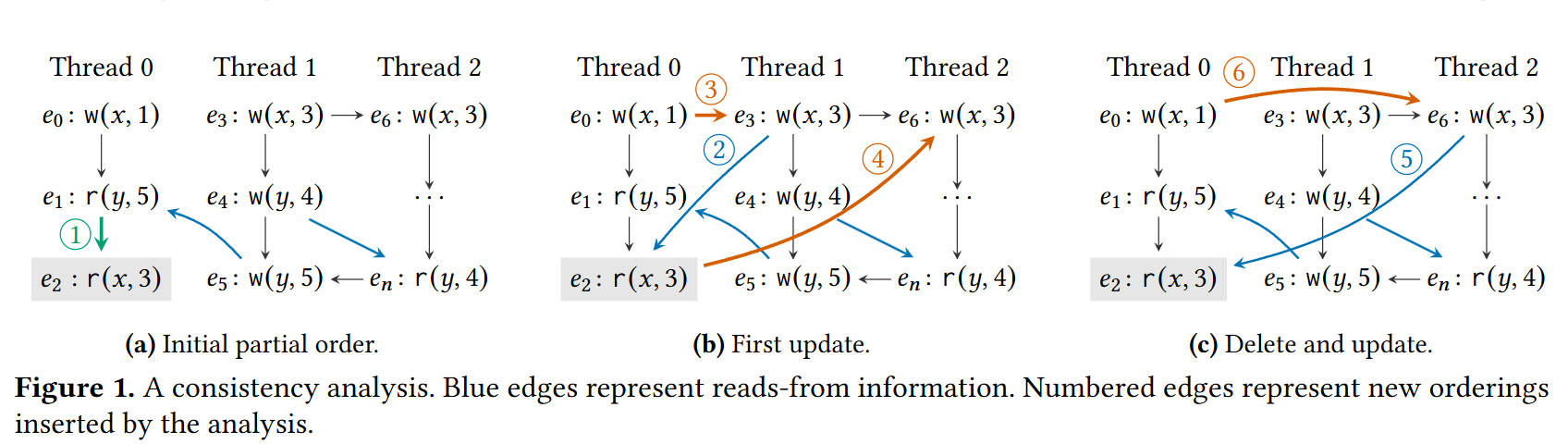
考虑一个包含 k=2 条链的链式DAG G 。每条链可以看作是一个线程的事件序列，事件按其在线程内的发生顺序排列。为了表示 G 中两条链 t_1 和 t_2 之间的偏序关系，CSSTs 维护 每个事件在其他链上的最早可达的事件ID。

具体地，令数组 A_{t_2 t_1} 存储的是从 \langle t_1, j_1 \rangle 或其在 t_1 上的后续事件，到链 t_2 的最早的直接可达事件的序列ID j_2 。如果 \langle t_1, j_1 \rangle 或其在 t_1 上的后续事件都不能直接到达链 t_2 上的任何事件，则 A_{t_2 t_1}[j_1] = \infty 。也就是：

这里 \min(\emptyset) = \infty 。

基于上述表示，以下三种基础查询操作可以表示为：

• successor(⟨t1, j1⟩, t2)：查询事件 \langle t_1, j_1 \rangle 在链 t_2 中最早的后继事件。

  相当于查询 A_{t_2 t_1} 后缀最小值： \min(A_{t_2 t_1}, j_1) 。

• predecessor(⟨t2, j2⟩, t1)：查询事件 \langle t_2, j_2 \rangle 在链 t_1 中最晚的前驱事件。

  相当于找满足 A_{t_2 t_1}[i] \le j_2 的最大索引 i ，可以线段树上二分。

• reachable(⟨t1, j1⟩, ⟨t2, j2⟩)：查询事件 \langle t_1, j_1 \rangle 是否可达事件 \langle t_2, j_2 \rangle 。

  相当于查询是否有 \text{successor}(\langle t_1, j_1 \rangle, t_2) \le j_2 。

动态可达性要求能够高效地插入和删除边。为了维护 A_{t_2 t_1} ，CSSTs 引入了额外的辅助数据结构：

对于链 t_1 上的每一个事件 \langle t_1, j_1 \rangle ，维护一个小根堆 edgeHeap21[j1]，存储所有从 \langle t_1, j_1 \rangle 直接指向链 t_2 的事件 \langle t_2, j_2 \rangle 的序列ID j_2 。这样，edgeHeap21[j1] 的堆顶就是从 \langle t_1, j_1 \rangle 直接到达链 t_2 的最早事件。

那么修改操作可以利用小根堆进行，插入和删除边就是在对应的小根堆中插入删除元素。然后只需要更新堆顶到线段树就好了。

通用的做法

当 k > 2 时，仅仅维护 k(k-1) 个 A_{t_2 t_1} 数组并不能直接解决问题。这是因为可达性可能通过多个中间链进行传递。例如，事件 \langle t_1, j_1 \rangle 到 \langle t_4, j_4 \rangle 的路径可能经过 t_2 和 t_3 ：

A_{t_2 t_1} 数组只记录 t_1 和 t_2 之间的直接边，不能直接捕捉这种跨越多链的传递关系。论文提出了两种策略来解决这个问题，分别对应完全动态和纯增量设置：

Fully Dynamic CSSTs

支持插入、删除。

每次查询进行传递闭包求全源最短路，线段树查询复杂度 \mathcal O(\min(\log n, d)) ，查询总复杂度 \mathcal O(k^3 \min(\log n, d)) 。

另外地，如果使用动态开点，更新复杂度可以降为 \mathcal O(\max(\log \delta, \min(\log n, d))) ，其中 \delta 是最大出度（交叉链密度）。

Incremental CSSTs

仅支持插入。

A_{t_2 t_1} 数组不再只存储直接边，而是直接存储所有传递可达性。也就是说，如果 \langle t_1, j_1 \rangle \rightarrow^* \langle t_2, j_2 \rangle ，那么 A_{t_2 t_1}[j^\prime_1] \le j_2 对于某个 j^\prime_1 \ge j_1 成立。这样查询直接在线段树查询，复杂度 \mathcal O(\min(\log n, d)) 。

这时候插入需要维护传递闭包，论文提出了一个扩散的过程（虽然我觉得就是朴素地更新）：

1. 对于所有可能的起始链 t^\prime_1 \in [k] ，找到 \langle t_1, j_1 \rangle 在 t^\prime_1 中的最晚前驱 ⟨t^\prime_1, j^\prime_1⟩
2. 对于所有可能的目标链 t^\prime_2 \in [k] ，找到 \langle t_2, j_2 \rangle 在 t^\prime_2 中的最早后继 ⟨t^\prime_2, j^\prime_2⟩
3. 然后，对于每一对 (⟨t^\prime_1, j^\prime_1⟩,⟨t^\prime_2, j^\prime_2⟩) ，检查是否已经存在一条路径。如果没有，将在线段树上将新的传递边 ⟨t^\prime_1, j^\prime_1⟩\to⟨t^\prime_2, j^\prime_2⟩ 插入到相应的 A_{t^\prime_2 t^\prime_1} 数组中。

这个过程会遍历 \mathcal O(k^2) 对链，在线段树上的操作都是 \mathcal O(\min(\log n, d)) ，所以总插入复杂度为 \mathcal O(k^2 \min(\log n, d)) 。

性能测试

横向比较了：

• Graphs 标准图表示。
• VCs 标准向量时钟表示。
• STs 基于普通线段树。

CSSTs 在大多数情况下优于 VCs 和 STs，尤其是在非流式或需要删除操作的场景。性能提升主要归因于其高效处理稀疏性，这不仅减少了运行时间，还降低了内存占用，使其能够处理 VCs 和 STs 因内存不足而失败的基准测试。在 C11 数据竞争检测等少数场景中，VCs 在没有显著传播的更新操作下表现更好，因为其更新成本接近 \mathcal O(1) 。但在需要传播的场景中，CSSTs 仍占优势。

后记

这个怎么感觉就只是在前人的线段树上加了点小 trick 呀（

发表信息：ASPLOS’24

作者信息：Hünkar Can Tunç, Ameya Prashant Deshmukh, Berk Cirisci, Constantin Enea, and Andreas Pavlogiannis.

关键词：并发分析, Happens-Before, 偏序, 动态可达性, 线段树