论文内容:使用KDT,构建拦截表放入R-tree的筛选方法进行预处理,加速查询过程。
算法总流程
预处理部分:
- 计算 V 的KD-Tree与Voronoi图。
- 对于 E,F 计算拦截器,填到拦截表中,并计算外边框。
- 对于每个 V ,将能够拦截器的元素(的外边框)插入R-tree中。
整体是 O(N_VM_{E+F}) 的,其中 N_V 为点的数量, M_{E+F} 为边与面的数量。
查询部分:
- 在KDT中找到距离 p 最近的点 v 。
- 在R-tree中遍历 v 能够拦截的元素,更新距离最小值。
常数很小。
筛选
通过KDT来找到最近的顶点后,需要找到最近的网格面,我们可以通过预处理一些筛选加快这个过程。
拦截
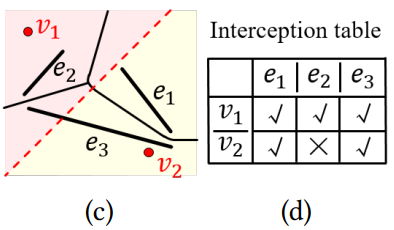
如图,实线表示三条边的Voronoi图的边,虚线表示两个点的Voronoi图的边。对于查询点 q :
- 如果距离 v_1 近,距离最近的线段可能为 e_1,e_2,e_3 。
- 如果距离 v_2 近,距离最近的线段可能为 e_1,e_3 。
差别在于边Voronoi图的顶点完全在点Voronoi边的一侧。于是可以看成对边的一个筛选?
这样的筛选称为 v 拦截了边 e ,数学地表述就是 \text{Cell}(v;\mathcal V_V)\cap \text{Cell}(e;\mathcal V_E)\neq \emptyset ,称 v 是 e 的拦截器,然后可以列出上面的拦截表。
以上是二维情况,推广到三维情况,有:
- 若 \text{Cell}(v;\mathcal V_V) \cap \text{Space}^\bot(e) \sub \text{Bisect}^v(v,l_e) ,则 v 不能拦截 e 。
这里 \text{Space}^\bot(s) 表示垂直于 s 的子空间, \text{Bisect} 解释见图解 Fig.5, l_e 表示 e 所在直线。
凸多面体
三维空间中还有面元的存在,直接使用上面的定义会比较难以表示。
我们注意到 \text{Cell}(v;\mathcal V_V) \cap \text{Space}^\bot(f) 是一个凸多面体,而 \text{Bisect}^v(v,\pi_f) 是凸的抛物面,如果判断在内部,可以直接判断顶点就可以了。
于是我们定义 \text{ConvexPoly}(v,e)=\text{Cell}(v;\mathcal V_V)\cap \text{Space}^\bot(e) ,记其 k 个顶点为 {x_i}_{i=1}^k ,于是 \text{ConvexPoly}(v,e) \sub \text{Bisect}^v(v,l_e) 就等价于 x_i\in \text{Bisect}^v(v,l_e) ,也就是 ||x_i-v||\leq \text{Dist}(x_i,l_e) ,其中 \text{Dist}(x,l) 表示点 x 到 l 的距离。
这样定义就很好实现,也方便推广到面的情况:
令 \text{ConvexPoly}(v,f)=\text{Cell}(v;\mathcal V_V)\cap \text{Space}^\bot(f) 的 k 个顶点为 {x_i}_{i=1}^k ,若 ||x_i-v||\leq \text{Dist}(x_i,\pi_f) ,则 v 不能拦截 f ,其中 \text{Dist}(x,\pi) 表示点 x 到平面 \pi 的距离。
R-tree
通过上面方法可以计算出拦截表,但是直接对拦截表进行遍历太低效了。
由上一节内容知, v 能拦截 e (也可以替换为 f )可以写为 \text{ConvexPoly}(v,e) \cap \text{Bisect}^e(v,l_e) \neq \emptyset (注意这里 \text{Bisect} 取边所在的部分),我们将左边的式子定义为 \text{Region}(v,e) 。但可惜这个区域不一定是凸的,很难直接判断在内部或外部,于是可以用边界盒来包住 \text{Region} ,然后对于一个点建立R-tree。
实现
使用泛洪算法:

图解
个人感觉这篇论文的图很帅。
Fig.3
-
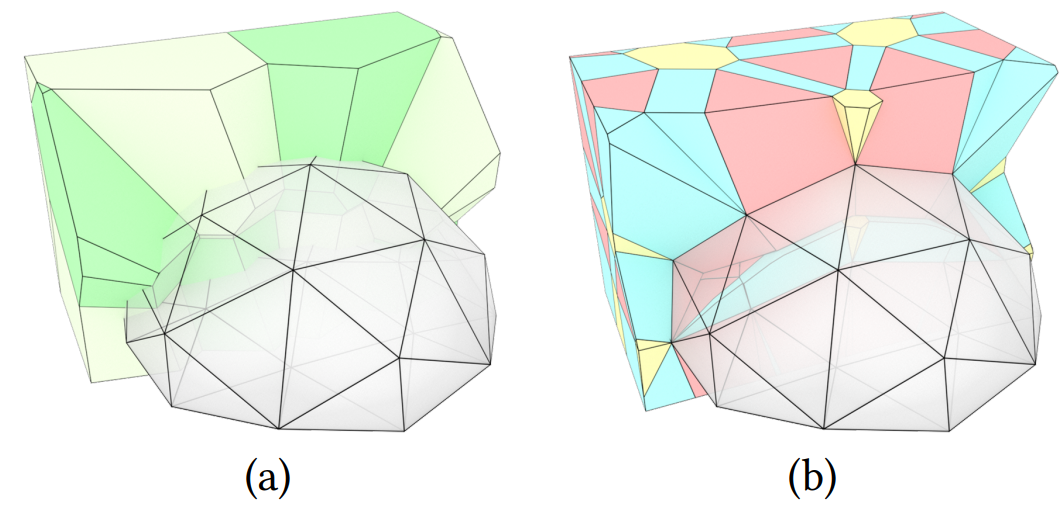
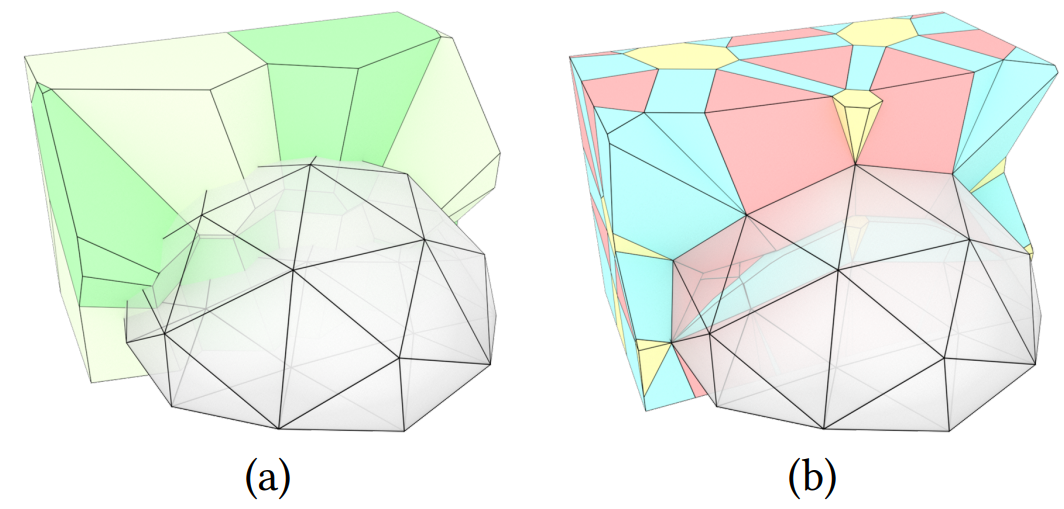
(a) 是由顶点生成的 Voronoi 图 \mathcal V_V 。
-
(b) 是由顶点、边、面生成的 Voronoi 图 \mathcal{V}_{V,E,F} ,对应关系:黄色-顶点、蓝色-边、红色-面。
Fig.4
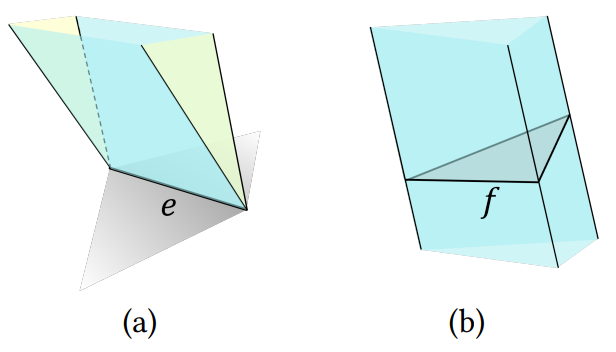
描述边和面交接处 \text{Cell} 的形状:面 \text{Cell} 的边垂直于面。边 \text{Cell} 的形状取决于相邻的平面。
Fig.5
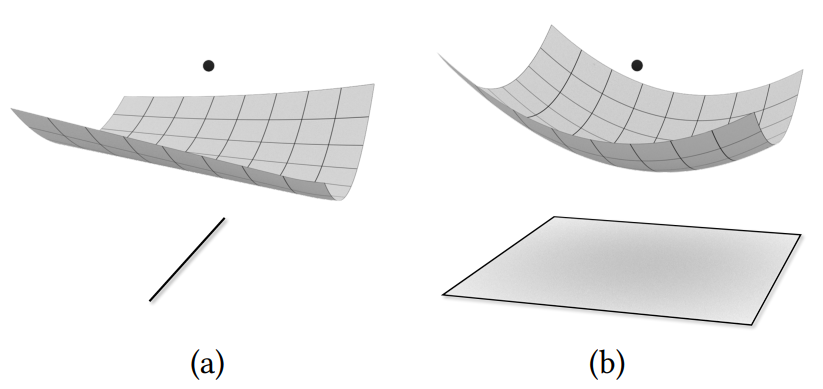
点到直线和点到平面的平分面(点到点为平面),记为 \text{Bisect}^v(v,l_e),\text{Bisect}^e(v,l_e);\text{Bisect}^v(v,\pi_f),\text{Bisect}^f(v,\pi_f) 。
Fig.6
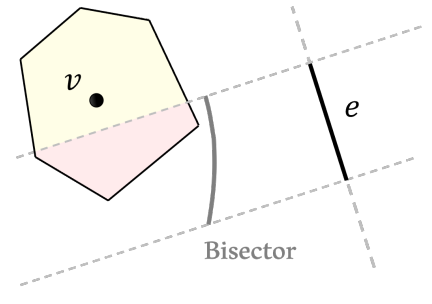
图中 e 所在的虚线为 l_e ,垂直于 e 的两条虚线表示 \text{Space}^\bot(e) 的边界;黄色部分表示 \text{Cell}(v;\mathcal V_V) ;粉色部分表示 \text{Cell}(v;\mathcal V_V) \cap \text{Space}^\bot(e) ;灰色实线表示 \text{Bisect}^v(v,l_e) 的边界的一部分,其左侧部分为此 \text{Bisect} 。
用来解释定理3:若 \text{Cell}(v;\mathcal V_V) \cap \text{Space}^\bot(e) \sub \text{Bisect}^v(v,l_e) ,则 v 不能 拦截 e ,也就是 v 在的 \text{Cell} 恰好在抛物面内部。
Fig.8
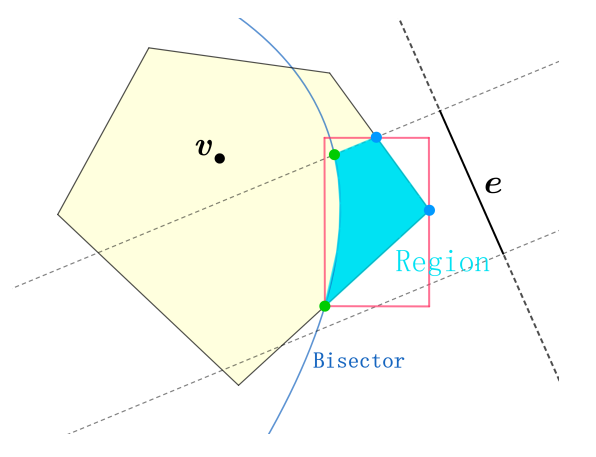
上文定义的 \text{Region} 部分,使用了外边框来包住,放入R-tree中。
Fig.9
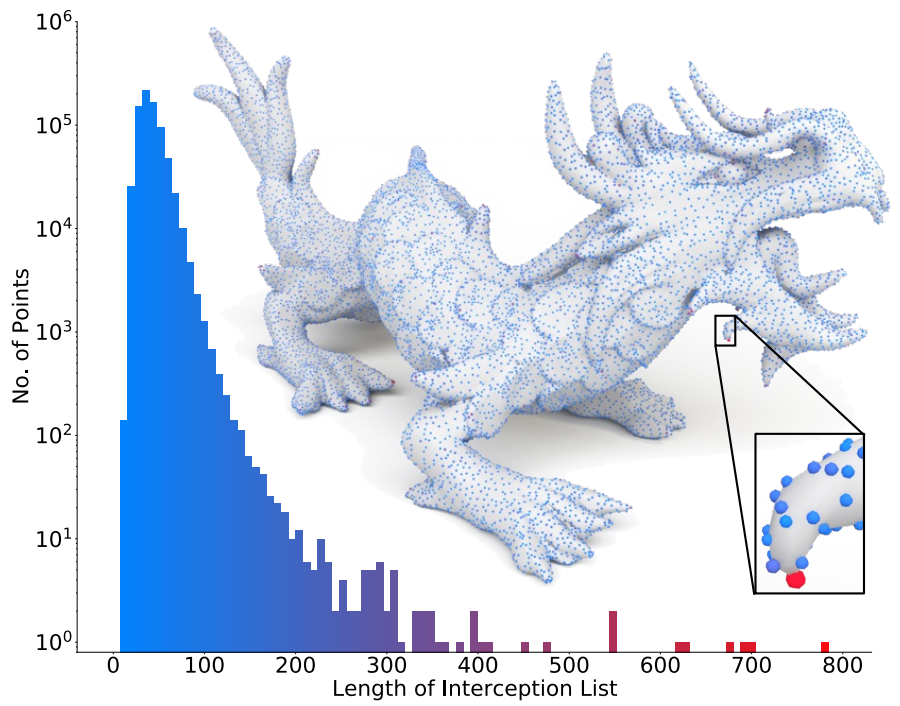
每个边的拦截元素数量不相同,对于1500K个面的物体,拦截元素数量统计如上。
Fig.10
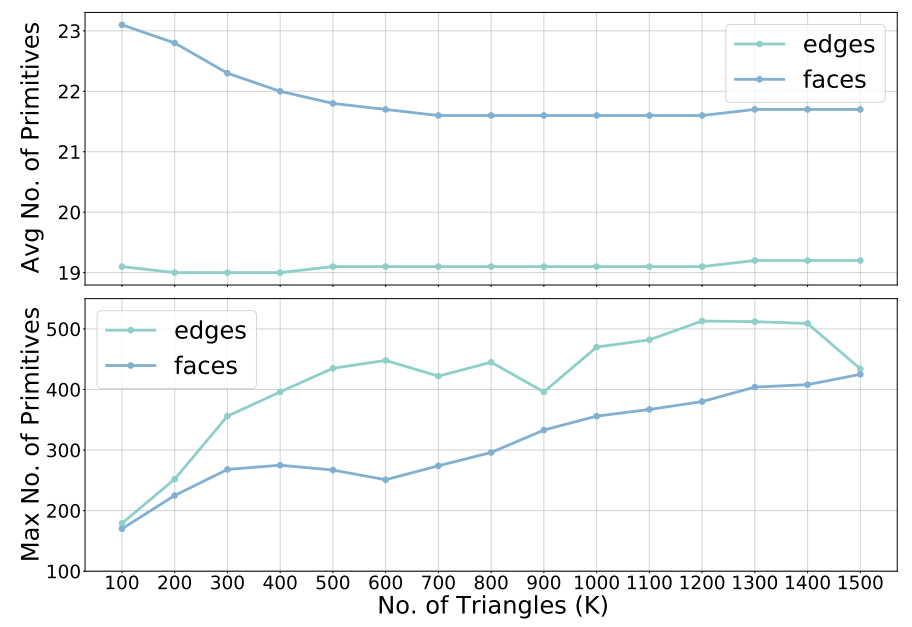
拦截数量的平均值与最大值随三角形数变化的曲线图(龙模型),可见平均拦截数相当少,算法期望运行时间还是很优秀的(
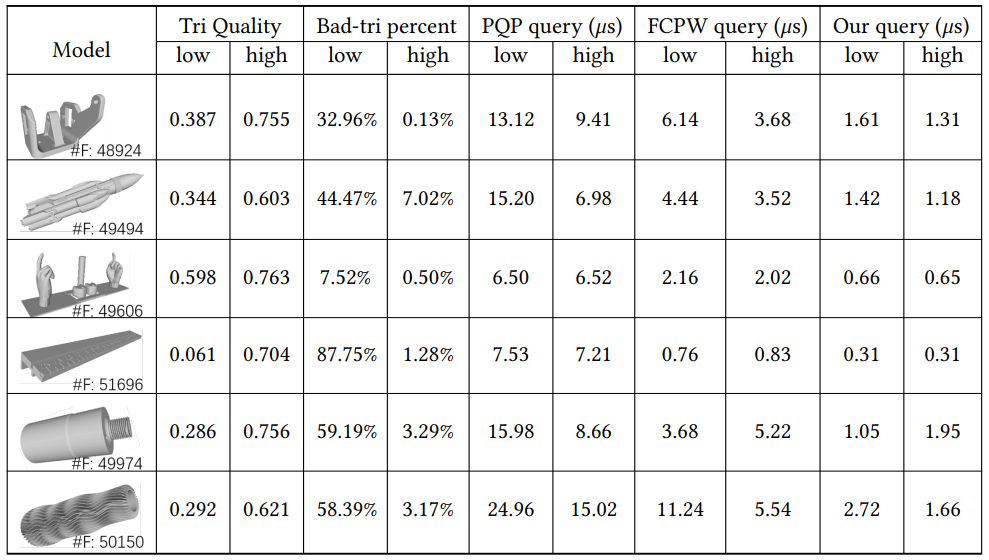
剩下表格基本为性能测试,这里不作解释。
方法评价
性能
预处理过程中计算拦截表的部分占用了 80\% 以上的时间:
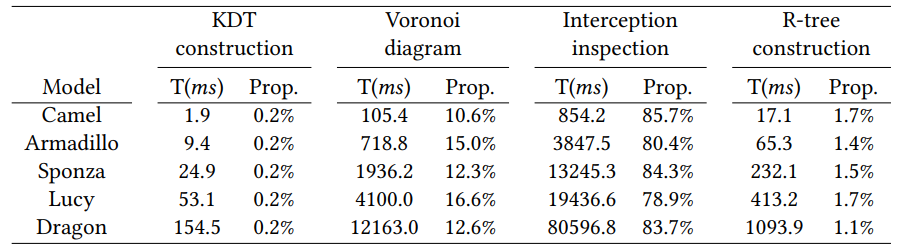
但查询时间相当优秀,比现有方法如 PQP、FCPW 要优秀得多:
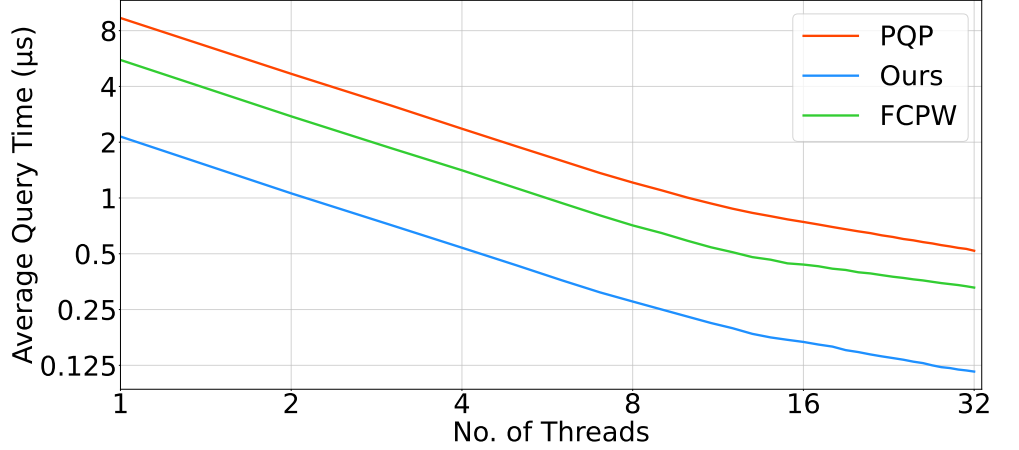
且对于较差的三角面上仍有较好的性能:
优缺点
- 优点:快。
- 缺点:
- 对于高度对称的形状,拦截表长度较大。例如物体为球面时,每个顶点都会拦截几乎全部三角形。
- 仅支持查询最近距离,相对于PQP还支持线面相交与碰撞算法较为单薄。
作者给出的改进方向:由于大部分顶点都无法被拦截,可以考虑改进过滤技术。