先来说一说组合数的概念

C^n_m \rightarrow 从 m 个物品中选 n 个物品，共有多少种方案

二项式系数

(a + b)^1 = C^0_1a + C^1_1b (a + b)^2 = C^0_2a^2 + C^1_2b + C^2_2b^2 (a + b)^3 = C^0_3a^3 + C^1_3a^2b + C^2_3ab^2 + C^3_3b^3 \cdots\cdots \begin{aligned}(a + b)^n &= C^0_na^n + C^1_na^{n - 1}b + \cdots + C^{n - 1}_nab^{n - 1} + C^n_nb^n\newline&=\sum_{i = 0}^nC^i_nx^{n - i}b^i\end{aligned}

感性理解：

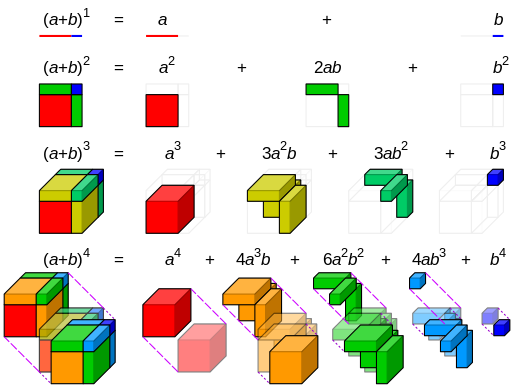
杨辉三角 & 递推求组合数

将其列成一个表:

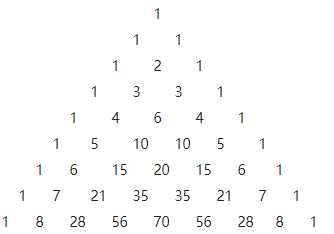
于是我们可以递推求出 C^n_m

C^n_m = C^{n - 1}_{m - 1} + C^{n}_{m-1}

*这里要注意边界情况（

时间复杂度: O(n^2)

代码

for i = 0 to n :
    C[i][0] = 1;
for i = 1 to n :
    C[i][i] = 1;

for i = 1 to n :
    for j = 1 to i :
        C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]);

下面是一些十分有趣的性质

一些性质

\sum_{i = 0}^nC_n^i=2^n

这个直观来看就是杨辉三角第 n 行的和

令 f(n) = \sum_{i = 0}^nC_n^i

\begin{aligned}f(n)&=\sum_{i = 0}^nC_n^i\newline&=\sum_{i =0}^n(C_{n-1}^{i-1}+C_{n-1}^{i})\end{aligned}

注意到每个 C_{n-1} 都被计算了两次

\begin{aligned}f(n)&=\sum_{i =0}^n(C_{n-1}^{i-1}+C_{n-1}^{i})\newline&=2\times \sum_{i = 0}^nC_{n-1}^i\newline&=2 \times f (n-1) \end{aligned} f(0) = 1 \Longrightarrow f(n) = 2^n

\sum_{i = 0}^kC^i_{n + i - 1} = C^{k}_{n + k}

直接根据杨辉三角感性理解 /cy

快速求组合数

C^k_n={n\times (n - 1) \times \cdots (n - k + 1) \over k\times (k-1)\times \cdots \times 1} = \prod_{i=1}^k{n-i+1\over i}

可以保证每一步运算都是整数

可以单次 O(n) 计算组合数模任意数

记录组合数因子出现次数 \text{cnt}(x) , 若知道每个数x的最小质因子 \text{mnp}(x)

从后往前扫 对于每个合数 将 \text{cnt}({x\over\text{mnp}(x)})+=\text{cnt}(x),\text{ } \text{cnt}(\text{mnp}(x))+=\text{cnt}(x)

最后可以得到质因数分解形式 由于质数个数 O({n \over \ln n}) 最终复杂度 O(n)

---

C_n^k={n!\over k!\times (n-k)!}

对于质数 可以 O(n) 预处理 O(1) 求值

如果n太大了怎么办？

可以直接 Lucas定理 (注意模数必须是质数)

如果模数也很大怎么办？

比如 n,m \le 10^9 ,P = 10^9+7

分块打表

为了快速获得 x!

设置 B 打表 B! , (2B)! , (3B)! …

每次查询一个 x! 只需要用表中最接近的值 O(B)

计算表的长度 O({P\over B})

如果模数不是定值怎么办？

不会（

---

例题 1

一个正 n 边形 将其所有对角线连起来 一共有多少个交点

保证 n 是奇数 不存在三条对角线共点

对于任意的四个点,可以确定两条对角线,有一个交点

所有答案 C_n^4

例题 2

给定 a , b 两个数组, 求

\sum_{i = 1}^n\sum_{j = i + 1}^nC_{a_i+a_j+b_i+b_j}^{a_i+a_j} a_i,b_i\le 2000;n\le 2\times 10^5

考虑 C_{n+m}^n 的组合意义

C_{n+m}^n \rightarrow 从 (0,0) 走到 (n,m) 的方案数

考虑 C_{a_i+b_i+a_j+b_j}^{a_i+b_i} 的组合意义

C_{a_i+b_i+a_j+b_j}^{a_i+b_i} \rightarrow 从 (0,0) 走到 (a_i+a_j,b_i+b_j) 的方案数

从 (-a_i,-b_i) 走到 (a_j,b_j) 的方案数

考虑计算任意 (-a_i,-b_i) 到任意 (a_i,b_i) 的方案数

减去重复计算的就好了

用 dp 可以做到 O(\max(a_i,b_i)^2)

例题 3

给你一棵 n 个节点的有根树。你要给每个节点分配一个 1\to n 的数字，使得每个节点分配的数字不同，并且每个节点分配的数字都是它子树内最小的。求方案数

考虑树形dp

dp(x) 表示 x 这个子树分配 1\to sz(x) 的方案数

考虑状态转移

dp(x)=C_{sz(x)-1}^{sz(u_1), sz(u_2),\cdots, sz(u_r)}\prod dp(u_i)

进一步推导:

\text{ans}=n!\prod{1\over sz(i)}

基础组合问题

加法原理

要么 A 要么 B (A和B不相交)

一个整数可以属于 [1,3] 或 [4,6] 那么共有 6 种可能

乘法原理

A\times B A 和 B 中各选一个

第一个整数属于 [1,3] 第二个整数属于 [1,2] 共有 6 种可能

栗子:

求有 2n 个点的二分图最多有多少条边?

显然一边 n 个点, 另一边 n 个点

左边的每一个点可以于右面的 n 个点相连

故 \text{ans}=n\times n = n^2

栗子 2:

n 个未知数，给定每个数的上限 a_i ，问你有多少种方法使得这些未知数都是正整数且互不相同。输出方案数模 10^9+7

考虑将 a_i 从小到大排序 依次确定未知数的值

\text{ans} = a_1 \times (a_2-1) \times (a_3-2) \times \cdots \times (a_n - (n - 1))

一个很有用的计数原则

一个由计数对象组成的集合 S ，要计算它的大小 |S| ，考虑如果我们找到一个集合 T ，使得 S 的元素与 T 的元素一一对应，那么 |S|=|T|

一个推广

如果 S 的每个元素对应到 a 个 T 中的元素， T 的每个元素对应到 b 个 S 中的元素，那么有

a|S|=b|T| ; |S|=|T|\times b/a

---

接下来我们就要讲讲最重要的 \text{Twelvefold way}

Twelvefold way

n 个有标号/无标号的球分给 m 个有标号/无标号的盒子

盒子有三种限制： A. 无限制 B. 每个盒子至少有一个球 C. 每个盒子至多有一个球

共 12 种问题

为了方便 将有标号记为 \text{L(labelled)} 无标号记为 \text{U(unlabelled)}

那么一个问题可以用缩写代替 如 UUA

(LLA) n 个有标号的球分给 m 个有标号的盒子

m^n.

(ULA) n 个无标号的球分给 m 个有标号的盒子

等同于方程的整数解个数

C_{n+m-1}^{m-1}

(ULB) n 个无标号的球划分给 m 个有标号的盒子 不能有空盒

等同于方程的整数解个数

C_{n-1}^{m-1}

(LLC) n 个有标号的球分给 m 个有标号的盒子 每个盒子至多放一个球

m!\over (m-n)!

(ULC) n 个无标号的球分给 m 个有标号的盒子 每个盒子至多放一个球

C_m^n

(LUC) n 个有标号的球分给 m 个无标号的盒子 每个盒子至多放一个球

[n\le m]

(UUC) n 个无标号的球分给 m 个无标号的盒子 每个盒子至多放一个球

[n\le m]

中间插播一下容斥 (

|A \cup B| = |A| + |B| - |A \cap B| |A\cup B\cup C| = |A| + |B| + |C| - |A\cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C| \left|\bigcup_{i=1}^nA_i\right|=\sum_{i=1}^n|A_i|-\sum_{1\le i \le j\le n}|A_i\cap A_j|+\cdots+\sum_{1\le i\le j\le k}|A_i \cap A_j \cap A_k|-\cdots+(-1)^{n-1}|A_1\cap \cdots \cap A_n|

(LLB) n 个有标号的球划分给 m 个有标号的盒子 不能有空盒 使用容斥原理：

\sum_{i = 0}^m(-1)^i n ^{m-i}C_m^i

(LUB) n 个有标号的球划分给 m 个无标号的盒子 不能有空盒

(LLB) 的答案再除以m!

(LUB) 即 n 个有标号的球划分给 m 个无标号的盒子 不能有空盒

第二类斯特林数.

S(n,k)={1\over k!}\sum_{j=0}^k(-1)^{k-j}C_k^j j^n

(LLB) 即 n 个有标号的球划分给 m 个有标号的盒子 不能有空盒

S(n,k)\times k!

(LUA) n 个有标号的球划分给 m 个无标号的盒子

枚举有几个盒子被分配了

\text{ans} = S(n,0)+S(n,1)+\cdots+S(n,m)

插播 \times 2 : 划分数

p(n,k) 划分数

n=x_1+x_2+\cdots+x_k

将 n 划分为 k 个正整数的方案数 方案与 x 的顺序无关

4 = 1 + 1 + 1 + 1
  = 2 + 1 + 1
  = 2 + 2
  = 3 + 1
  = 4

递推式

考虑最小的数是否为 1

p(n,k)=p(n-k,k)+p(n-1,k-1)

那么剩下的 UUA 和 UUB 就很好解决了

(UUB) n 个无标号的球划分给 m 个无标号的盒子 每个盒子至少有一个球

p(n,m)

(UUA) n 个无标号的球划分给 m 个无标号的盒子

枚举有几个盒子被分配了

p(n,1)+p(n,2)+\cdots+p(n,m) p(n+m,m)

ABC三种限制的意义

A）无限制 (labelling)

将每个元素标号 放进第i个盒子就标为i号（当盒子有标号时 无标号时和B类似）

B）每个盒子至少有一个球 (grouping)

将所有元素分成m组 放进同一个盒子的是同一组

C）每个盒子至多有一个球 (selection)

为每个球选一个盒子