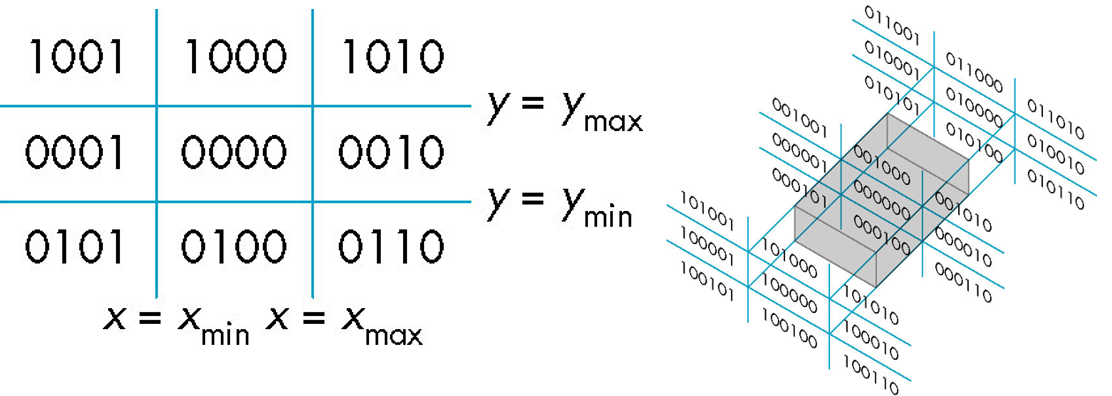Foundation of mathematics

Vector space and affine space

• 元素与操作 Elements and operations

• 仿射和与凸性：意义、证明及应用 Affine sum and convexity: meaning, proof, and use

  仿射和是形式为 P = \alpha_1 P_1 + \alpha_2 P_2 + \dots + \alpha_n P_n 的点的组合，其中 \alpha_1 + \alpha_2 + \dots + \alpha_n = 1 。

  凸对象的定义是：对于对象中的任意两点，其连线的所有点也在该对象中。凸包是包含所有给定点的最小凸集合，应用包括几何建模和可视化。

• 正确与不正确的表达式 Valid and invalid expressions

  表达式如 P + Q 是不合法的，因为两点不能直接相加。合法的表达式包括点与向量的加法或点与点的减法。

• 表示法 Representation

  • 齐次坐标：意义与用途 Homogenous coordinates: meaning & use

  • 在不同坐标系间切换时点坐标的计算 Point coordinates computation when switching to different coordinate system

Geometry

• 几何基元：线、多边形、平面、曲线 Geometric primitives: Line, polygon, plane, curve

• 表示法：参数式、显式、隐式 Representation: parametric, explicit, implicit

• 构造：线（由两点定义），平面（由三点、一点和法向量、一点和两个矢量定义），曲线（由控制点、控制点和切向矢量定义）Construction: line (2 points), plane(3 points, 1 point and normal, 1 point and two vectors), curve (control points, control points and tangent vectors)

• 属性：法向量（平面、曲线），切线和曲率（曲线） Properties: normal (plane, curve), tangent and curvature (curve).

• 相交计算：（线-线），（线-面），（曲线-面） Intersection computing: (line line), (line plane), (curve, plane)

Transformations

• 平移、缩放、旋转、剪切、正交和平行投影的矩阵形式 Matrix form for translate, scale, rotation, shear, planar projection(ortho, perspective).

  1. 平移 (Translation)： 平移变换使用齐次坐标中的平移矩阵进行表示： T(x, y, z) = \begin{bmatrix} 1 & 0 & 0 & dx \newline 0 & 1 & 0 & dy \newline 0 & 0 & 1 & dz \newline 0 & 0 & 0 & 1 \end{bmatrix} 其中 (dx, dy, dz) 是平移向量。

  2. 缩放 (Scaling)：
     缩放变换用对角矩阵表示： S(sx, sy, sz) = \begin{bmatrix} sx & 0 & 0 & 0 \newline 0 & sy & 0 & 0 \newline 0 & 0 & sz & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix} (sx, sy, sz) 分别表示沿 x、y、z 方向的缩放因子。

  3. 旋转 (Rotation)：
     旋转矩阵分为绕各轴的旋转：

     • 绕 x -轴： R_x(\theta) = \begin{bmatrix} 1 & 0 & 0 & 0 \newline 0 & \cos\theta & -\sin\theta & 0 \newline 0 & \sin\theta & \cos\theta & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix}
     • 绕 y -轴： R_y(\theta) = \begin{bmatrix} \cos\theta & 0 & \sin\theta & 0 \newline 0 & 1 & 0 & 0 \newline -\sin\theta & 0 & \cos\theta & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix}
     • 绕 z -轴： R_z(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta & 0 & 0 \newline \sin\theta & \cos\theta & 0 & 0 \newline 0 & 0 & 1 & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix}

  4. 剪切 (Shear)：
     剪切矩阵的形式因方向不同而有所区别，例如： Sh(x, y) = \begin{bmatrix} 1 & sh_{xy} & sh_{xz} & 0 \newline sh_{yx} & 1 & sh_{yz} & 0 \newline sh_{zx} & sh_{zy} & 1 & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix}

  5. 投影 (Projection)：

     • 正交投影 (Orthographic Projection)： P_{ortho} = \begin{bmatrix} 1 & 0 & 0 & 0 \newline 0 & 1 & 0 & 0 \newline 0 & 0 & 0 & 0 \newline 0 & 0 & 0 & 1 \end{bmatrix}
  • 透视投影 (Perspective Projection)： P_{persp} = \begin{bmatrix} 1 & 0 & 0 & 0 \newline 0 & 1 & 0 & 0 \newline 0 & 0 & 1 & -1/d \newline 0 & 0 & 1/d & 0 \end{bmatrix} d 为视点到投影平面的距离。

  

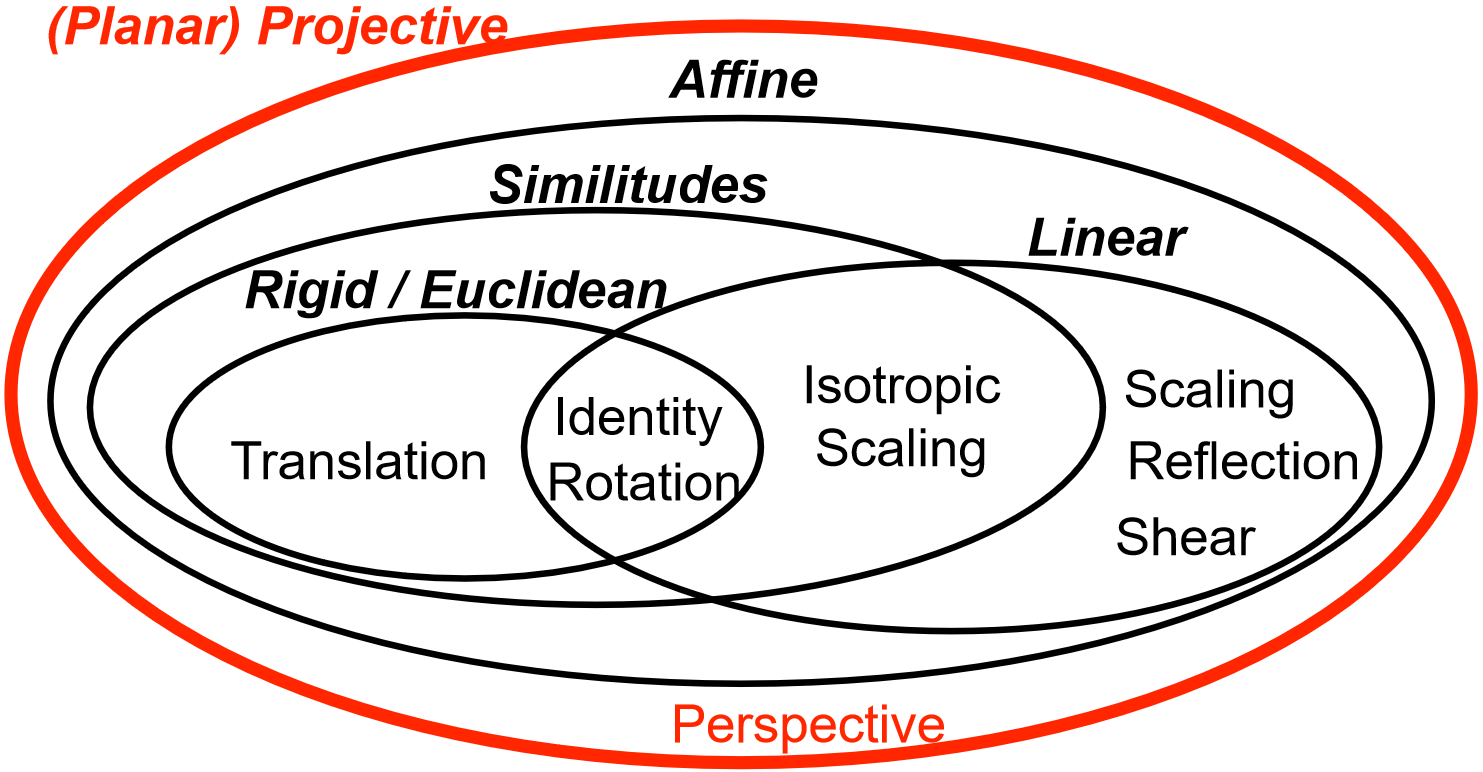
  线性变换和平移组合称为仿射变换。仿射变换保持平行性和平直性。

  欧式变换加均匀缩放变换称为相似变换。相似变换保持长度比、夹角。

  多个仿射变换和多个相似变换连乘，结果一定为仿射变换。

• 作为群的变换：子群及其对应特征 Transformations as group: subgroup and corresponding characteristics

  变换矩阵集合构成一个群，满足封闭性、结合性、单位元存在性和逆元存在性。旋转变换构成一个特殊正交群 SO(3) ，其特征为矩阵的行列式等于1。

• 变换的逆矩阵 Inverse matrix of transformation

  • 平移：将平移向量反号。
  • 缩放：缩放因子取倒数。
  • 旋转：旋转矩阵的逆矩阵是其转置矩阵。

• 通过多个矩阵的连接实现复杂变换 Implementing complicated transformation by concatenation of multiple matrices

  假设我们先进行缩放变换 S ，然后进行旋转变换 R ，最后进行平移变换 T ，那么组合矩阵为： M=T\cdot R\cdot S

• 平滑旋转 Smooth rotation

  • 四元数与旋转之间的转换 Switch between quaternions and rotation

  四元数形式 q = w + xi + yj + zk ，与旋转轴和角度的关系为： q = \cos\frac{\theta}{2} + (\sin\frac{\theta}{2})(xi + yj + zk)

  四元数可以直接用于计算旋转矩阵，避免传统方法中的奇异性。

  • 使用球面线性插值（slerp）进行平滑旋转 Using slerp to do smooth rotation Slerp(q_1, q_2, t) = \frac{\sin((1-t)\Omega)}{\sin(\Omega)}q_1 + \frac{\sin(t\Omega)}{\sin(\Omega)}q_2 其中 \Omega = \arccos(q_1 \cdot q_2) 表示四元数间的夹角。

Basic concepts and knowledge

• 图像形成流水线 Pipeline of image formation

  • 每个过程的意义与任务 meaning and tasks in each process

  Pipeline architecture:

  （Modeling）Vertices -> 顶点处理 Vertex Processor -> 裁切和图元装配 Clipper and Primitive Assembler -> 光栅化 Rasterizer -> Fragment Processor -> （Frame buffer）Pixels

  1. 顶点处理 Vertex Processor：负责处理和转换顶点数据，准备用于下一步的计算。
     • 执行坐标变换，如从对象空间到世界空间再到摄像机（眼）空间最后到裁剪空间。
     • 计算光照效果，比如通过Phong反射模型确定每个顶点的颜色。
     • 应用变形动画，如果有的话。
  2. 裁切和图元装配 Clipper and Primitive Assembler：确保只有在视锥体内的几何体才会被进一步处理，并将顶点组装成基本几何元素。
     • 裁剪掉不在视锥体内的部分几何体，即移除不可见的部分。
     • 将顶点组织成几何图元，例如三角形、线段或多边形，以便后续光栅化处理。
  3. 光栅化 Rasterizer：决定哪些像素应该被着色，并为每个像素生成片段。
     • 确定哪些像素位于几何图元内部，并创建对应的片段。
     • 插值顶点属性，如颜色、纹理坐标和深度值，以赋予片段这些属性。
  4. Fragment Processor：对每个片段进行精细处理，最终确定像素的颜色。
     • 执行纹理映射，使用纹理图片来增加表面细节。
     • 应用各种着色算法，如环境遮挡、镜面高光等。
     • 执行隐藏表面消除（深度测试），保证正确的绘制顺序。

• 计算机图形学中的坐标系统 Coordinate systems in computer graphics

  • 物体、摄像机、纹理、参数化坐标系 Object, camera, texture, paramatric.

  物体坐标系 (Object Coordinate System)：每个物体都有自己的局部坐标系，也称为物体空间或模型空间。在这个坐标系中，物体的顶点和其他几何数据被定义。用途：当需要将物体放置到场景中时，会通过一个变换矩阵将物体坐标转换为世界坐标。

  世界坐标系 (World Coordinate System)：这是场景中的全局坐标系，所有物体的位置和方向都是相对于这个世界坐标系来定义的。用途：从物体坐标到世界坐标的转换通常由物体的变换矩阵完成，该矩阵可以包括平移、旋转和缩放等操作。

  摄像机坐标系 (Camera Coordinate System)：摄像机也有自己的坐标系，有时称为视图空间或眼睛空间。在这个坐标系中，所有的物体都相对于摄像机的位置和方向来描述。用途：从世界坐标到摄像机坐标的转换由视图变换矩阵完成，这个矩阵包含了摄像机的位置、朝向和上方向的信息。

  纹理坐标系 (Texture Coordinate System)：用于指定表面贴图上的特定位置。纹理坐标通常用(u, v)对来表示，类似于二维平面直角坐标系。用途：纹理坐标一般直接与物体表面的顶点关联，在渲染过程中不需要额外的坐标转换。

  参数化坐标系 (Parametric Coordinate System)：这是一种用于定义曲线和曲面的坐标系，特别是在非均匀有理B样条(NURBS)等复杂几何形状中。用途：参数化坐标系通常不会直接转换到其他坐标系；相反，它们用于计算实际的三维坐标，然后这些坐标再转换到其他坐标系中。

• 两种不同的图像形成方法 2 different image formation approaches

  • 图像空间和物体空间 image space and object space

  物体空间 (Object Space) 是指物体本身的坐标系，在这个空间中，物体被建模和定义。

  图像空间 (Image Space) 是指最终显示给用户的二维屏幕上的坐标系。它由经过一系列变换后的物体空间坐标转换而来，包括但不限于模型视图变换和投影变换。

  • 如何工作 how to

  Model-View Transformation -> Projection Transformation -> Perspective Division -> Clipping -> Projection

  1. 模型视图变换（Model-View Transformation）在这个阶段，所有的物体坐标被从世界坐标系转换到摄像机坐标系。这是通过组合平移、旋转和其他线性变换来实现的，以模拟摄像机的位置和方向。
  2. 投影变换 (Projection Transformation) 接下来，应用投影变换将摄像机坐标系下的坐标映射到规范化设备坐标（Normalized Device Coordinates, NDC）。这一步骤决定了如何“拉伸”或“压缩”空间，以适应特定类型的投影（如正交或透视）。
  3. 透视除法 (Perspective Division) 当采用透视投影时，需要执行透视除法。这是因为在透视投影中，齐次坐标系中的 w 分量不是 1 ，而是与 z 值有关的一个比例因子。为了得到NDC坐标，必须用 w 分量去除 x , y , 和 z 分量。（4D -> 3D）
  4. 裁剪 (Clipping) 裁剪是指检查哪些几何体位于视区内，并丢弃不在视区内的部分。这有助于减少渲染不必要的几何数据，提高效率。
  5. 投影 (Projection) 最后一步是将NDC坐标转换到实际窗口或屏幕坐标，使得图像可以在特定的窗口区域正确显示。这包括了视口变换（viewport transformation）。 (3D -> 2D)
  • 优缺点 advantages and disadvantages

• 局部与全局光照 Local and global illumination:

  • 局部和全局光照的意义 what’s local and global meaning

  局部光照模型（Local Lighting）是指只考虑直接光源对物体表面的影响，而不考虑环境中其他物体之间相互反射的光。这种模型通常计算速度较快，适合实时渲染，如游戏和交互式图形应用。

  全局光照模型（Global Illumination）则不仅考虑了直接光照，还包括了间接光照的效果，即场景中所有物体之间的多次反射、折射等现象。全局光照能提供更加真实的效果，但计算成本较高，通常用于电影制作和高质量的静态图像渲染。

  • 示例：Phong模型对比光线追踪 examples: phong vs. raytracing

  • Phong 模型可以快速地模拟漫反射、镜面反射和环境光。它在实时渲染中被广泛使用，因为它可以在硬件上高效实现。而光线追踪是一种更为复杂的渲染技术，通过追踪从摄像机出发的光线路径来模拟真实的光照效果。它可以处理全局光照效应，如阴影、反射、折射和散射，从而生成更逼真的图像，但是计算量非常大，不适合实时应用。

• 隐藏表面消除 Hidden surface removal

  • 两方面：背面剔除，隐藏表面消除 Two aspects: back face culling, hidden surface removal
  • 背面剔除基于：在封闭的物体中，面向内部的多边形（即背对摄像机的面）不会在最终图像中可见。通过检查每个多边形的法线方向与视线方向之间的关系来判断一个多边形是否为背面。如果多边形的法线指向远离摄像机的方向，则认为它是背面，可以安全地将其剔除而不影响最终渲染结果。
  • 隐藏表面消除解决了当多个多边形占据同一屏幕位置时的问题，即决定哪个多边形应该是最前面的，并因此显示出来。Z-buffer（深度缓冲）、画家算法（Painter’s Algorithm）、二叉空间分割树（BSP Tree）等实现。

• Blinn 和 Phong光照模型 Blinn & phong illumination model

  Phong光照模型是一种用于计算表面光照效果的模型，它由三个主要部分组成：环境光、漫反射和镜面反射： I=k_d I_d (\mathbf l\cdot \mathbf n)+k_s I_s (\mathbf v\cdot \mathbf r) ^\alpha +k_a I_a 其中：

  1. I 是最终颜色强度。
  2. k_d,k_s,k_a 分别是漫反射 diffuse reflection、镜面反射 specular reflection 和环境光 ambient light 的反射系数。 I_d,I_s,I_a 分别是光源的漫反射、镜面反射和环境光强度。
  3. \mathbf l 是从表面点到光源的单位向量、 \mathbf n 是表面法线的单位向量。
  4. \mathbf v 是从表面点到观察者的单位向量、 \mathbf r 是理想反射方向的单位向量。
  5. \mathbf \alpha 是高光指数（shininess coefficient），决定了镜面高光的锐度。

  Blinn光照模型使用半角向量来近似Phong模型中的镜面反射项，这在计算上更加高效。该模型同样包含环境光、漫反射和镜面反射： I=k_d I_d (\mathbf l\cdot \mathbf n)+k_s I_s (\mathbf n\cdot \mathbf h) ^\beta +k_a I_a 其中：

  1. \mathbf h 是半角向量，它是光源向量 \mathbf l 和观察者向量 \mathbf v 的平均单位向量。
  2. \beta 是用来匹配高光度的指数，通常与 Phong 模型中的 \alpha 相等或类似。
  • 矢量运算 Vector computation

  理想反射方向的单位向量 \mathbf{r} = \mathbf{l} - 2(\mathbf{l} \cdot \mathbf{n})\mathbf{n} ，半角向量 \mathbf{h} = \frac{\mathbf{l} + \mathbf{v}}{|\mathbf{l} + \mathbf{v}|} ，对于隐式定义的曲面法向量为梯度向量 \mathbf{n}=\nabla f 。

  • 差异 Differences

  Blinn模型引入了半角向量 \mathbf h ，减少了计算复杂度，并且通常提供更自然的高光效果。

• Phong 和 Gouraud 着色 Phong and Gouraud shading

  • 实现方式 Implementation

  Gouraud 着色是使用光照模型为每个顶点计算光照强度，对于两个顶点之间的边缘，使用线性插值来确定沿该边缘的光照强度，对于一个多边形内部的所有片段，根据相邻顶点的光照强度进行双线性插值以决定最终颜色。

  Phong 着色不是对光照强度进行插值，而是对法线向量进行插值。首先计算每个顶点的法线，然后在多边形的每个顶点之间，对法线向量进行插值（通过归一化使得高光过渡均匀），以得到多边形内部各片段的近似法线。在着色时使用插值得到的法线向量，在每个片段上应用光照模型计算光照强度与颜色。

  • 优点和缺点 Pros. and Cons.

  • Gouraud 着色大部分的光照计算都是在顶点级别完成的，因此计算量相对较小，适合硬件加速。但如果多边形较大或有强烈的镜面反射，可能会出现光强不连续的现象，导致“Gouraud阴影”或“ Mach带效应”，即沿着多边形边缘出现亮度突变。还会出现高光区丢失（位于多边形中心）、高光区不正常（位于多边形顶点、光源向多边形移动）的情况。

  • Phong 着色提供更精确和平滑的光照效果，特别是对于镜面反射和光滑曲面，能够更好地捕捉和显示曲面上的微小变化，从而提高视觉真实感。但每个片段都需要单独计算光照，这增加了计算量，可能不适合所有场景下的实时渲染。

• 锯齿现象 Aliasing

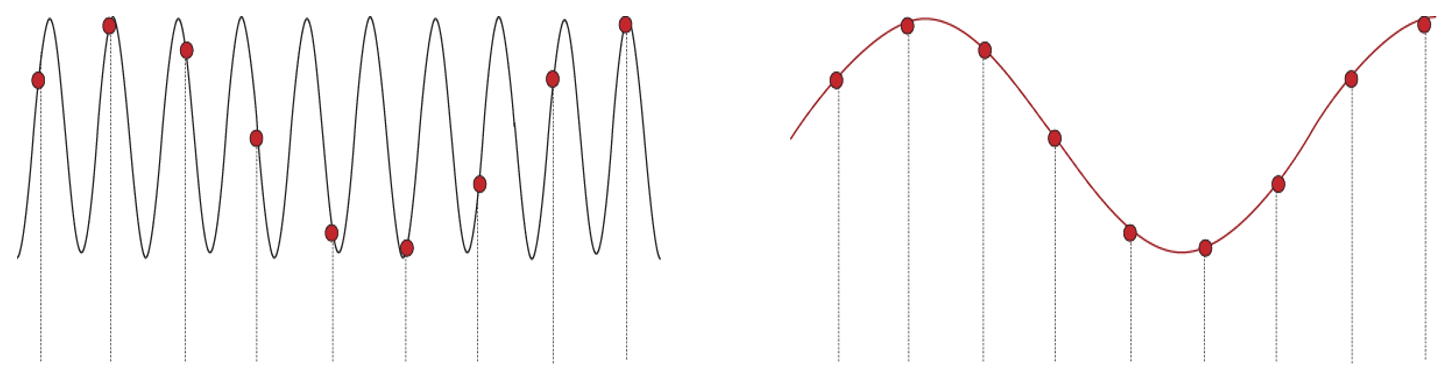
  • 采样、量化 Sampling, quantization.

  在信号处理中，将连续函数映射到离散形式的过程被称为采样。当我们将连续变量转换为离散值时，这一过程称为量化。例如，在使用计算机表示或渲染图像时，我们必须同时进行采样和量化。伽马校正可以帮助量化过程。采样密度足够的情况下，我们能够获得良好的结果；但如果采样不足，可能会导致重建过程中出现锯齿现象。

  

  • 至少两种不同的锯齿效应 Specifying at least 2 different aliasing effects

  • 这种类型的锯齿主要表现为方向性锯齿，通常出现在垂直和水平边缘上，而不是实际的斜率。这是因为直线在低分辨率下不能完美地表示，导致视觉上的阶梯状效果。

  • 当纹理图案在表面上重复时，如果这些图案的频率高于采样频率的一半（奈奎斯特频率），就会产生锯齿现象。这种情况下，纹理可能看起来像是错误的模式或颜色带，这比边缘锯齿更难解决，并且激发了对抗锯齿的有趣数学研究。

  • 超级采样，低通/卷积滤波 Super sampling, low pass/convolution

  • 超级采样：计算每个像素多个颜色值并取平均。问题：它只能将问题推得更远，因为信号仍然是非带限的。因此，仍然可能发生锯齿现象，特别是在信号和采样都是规则的情况下。

  • 低通/卷积滤波：以更高的分辨率计算图像，然后使用低通滤波器（如Box、Gaussian、bilinear、bicubic等）进行降采样到较低分辨率。每个输出的低分辨率像素是输入子样本的加权平均，权重取决于相对空间位置。例如，高斯滤波器作为距离的函数，或者方框滤波器在方形内部为1，在外部为0。

• 纹理映射 Texture mapping

  • 纹理映射、环境映射、凹凸映射 Texture mapping, environmental mapping, bump mapping

  纹理映射是一种将二维图像贴到三维物体表面的技术。它使得3D模型看起来更加真实，因为可以通过这种方式添加细节，如颜色、图案等，而不需要增加几何复杂度。纹理映射涉及到从2D纹理空间到3D对象表面的映射，这可能需要处理可展表面（Developable Surfaces）和非可展表面的问题，以避免变形。

  环境映射也称作反射映射（Reflection Mapping），是使用一张环境的图片作为纹理图，允许模拟高光泽度表面的效果。它通过创建一个虚拟的环境来反映在物体表面上，从而实现更真实的反射效果。

  凹凸映射是一种通过改变渲染过程中的法线向量来模拟表面细节的技术。它不是真正地改变物体的几何形状，而是让光照计算时表面看起来有起伏，增加了视觉上的深度感。

  • Mipmap, 区域采样 Mipmap, area sampling

  Mipmap 是一种用于减少锯齿现象的技术，当纹理被缩小显示时尤为有用。它通过构建一系列预过滤并重新采样的图像金字塔，每个层级对应不同的分辨率。在光栅化期间，选择与所需的采样密度最接近的Mip级别进行采样。

  区域采样是一种比点采样更优但速度较慢的方法，它通过对像素对应的纹理区域进行平均来获得更好的结果。这种方法可以解决由于简单点采样导致的锯齿问题。为了优化性能，通常会结合Mipmap技术，预先对不同级别的纹理进行模糊处理，即所谓的预过滤。

  

• 颜色 Color

  • 人类可见光谱范围 Spectrum range of human visible light

  可见光是电磁波的一部分，其波长范围大约在450至700纳米之间。光的颜色由其光谱决定，即每个波长的能量量。这构成了一个完整的分布，对于每一个波长都有一个值（无限数量的值）。

  • 加法和减法颜色系统 Additive and subtractive color system

  加法混色 (Additive color mixing)：通过组合光线产生一系列颜色。红、绿、蓝（RGB）是主要的加法颜色。等量混合三种基本色可以得到白光；两种等量的基本色混合可以创建补色。 减法混色 (Subtractive color mixing)：当颜色通过反射或透射物质时，会吸收某些波长并反射或透过其他波长。例如，在绘画或摄影中使用的颜料和滤镜遵循此规则。

  • 同色异谱和颜色再现 Metamers and reproduce of color

  同色异谱 (Metamers)：不同的光谱可能激发相同的锥体细胞反应，这意味着它们看起来一样，尽管物理上不同。这种现象使得用三个原色就可以重现所有颜色成为可能。

  颜色再现：由于人眼的视觉系统复杂性以及光谱信息被压缩成三个数值（对应于红L, 绿M, 蓝S三种类型的锥体细胞响应），可以通过选择适当的三个原色来匹配任何给定的目标颜色。L、M 和 S 锥体细胞的响应曲线并不是完全独立的；它们之间存在重叠。这意味着一个特定波长的光可以同时激发多个类型的锥体细胞，而且这些细胞之间的激发程度并不总是成比例的。

  • 颜色空间 Color space

  • CIE XYZ颜色空间：这是最广泛认可的颜色规格标准，基于色彩匹配实验。它使用了三个单色原色，并且避免了负数出现的问题。

  • RGB颜色空间：许多显示器和投影仪使用红、绿、蓝作为三原色。通过线性变换可以从XYZ颜色空间转换到特定设备的RGB颜色空间。

  • 色度图 (Chromaticity diagram)：为了简化三维颜色空间的可视化，通常会将其投影到二维平面上，比如 X+Y+Z=1 的平面。

• 参数曲线 Parametric curve

  • 插值、Hermite、Bezier、B样条曲线：概念与构造 Interpolating, hermite, bezier b-spline curve: concept, construction

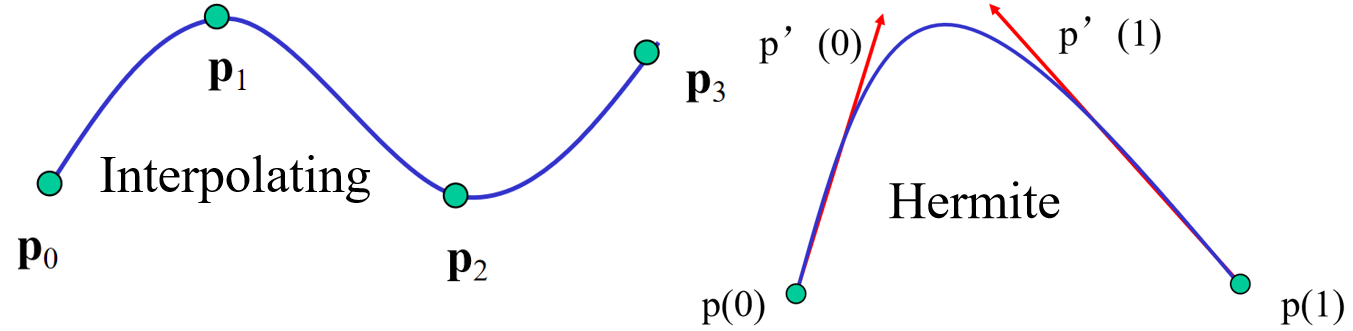
  • 插值曲线：例如给定四个控制点 p_0, p_1, p_2, p_3 ，插值曲线 p(u) = c_0 + c_1u + c_2u^2 + c_3u^3 为： \begin{aligned} p(0) &= p_0 = c_0 \newline p\left(\frac{1}{3}\right) &= p_1 = c_0 + \frac{1}{3}c_1 + \left(\frac{1}{3}\right)^2c_2 + \left(\frac{1}{3}\right)^3c_3 \newline p\left(\frac{2}{3}\right) &= p_2 = c_0 + \frac{2}{3}c_1 + \left(\frac{2}{3}\right)^2c_2 + \left(\frac{2}{3}\right)^3c_3 \newline p(1) &= p_3 = c_0 + c_1 + c_2 + c_3 \end{aligned} 然后解出曲线参数 c_0,c_1,c_2,c_3 。

  • Hermite 曲线：还规定了起点和终点处的切线方向。这样可以保证相邻曲线段之间的连续性和一阶导数的连续性。Hermite 形式通过两个端点位置 p(0)=p_0,\;p(1)=p_3 和两个端点处的导数 p'(0), p'(1) 来确定每一段三次曲线，系数矩阵 \mathbf{c} = \mathbf{M_H} \mathbf{q} 为： \mathbf{M_H} = \begin{bmatrix} 1 & 0 & 0 & 0 \newline 0 & 0 & 1 & 0 \newline -3 & 3 & -2 & -1 \newline 2 & -2 & 1 & 1 \end{bmatrix}\quad \mathbf{q} = \begin{bmatrix} p(0) \newline p(1) \newline p'(0) \newline p'(1) \end{bmatrix}

    

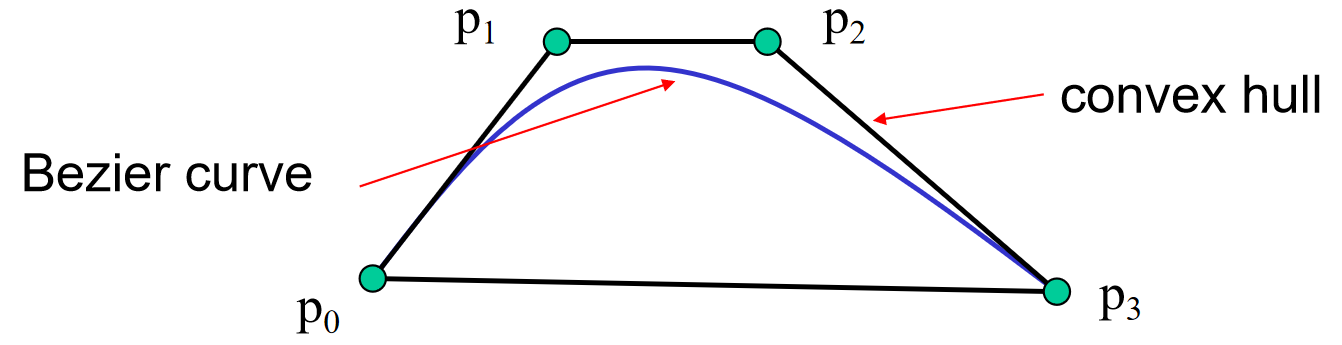
  • Bezier 曲线：基于 Bernstein 多项式的参数多项式曲线。它们由一组控制点定义，但并不一定通过所有的控制点。Bezier 曲线的一个重要特点是它们在起点和终点处会接触第一个和最后一个控制点，并且在这些点上的切线方向是由相邻的控制点决定的。 B(t) = (1-t)^3P_0 + 3(1-t)^2tP_1 + 3(1-t)t^2P_2 + t^3P_3, \quad t \in [0, 1]

    

  • B样条曲线：Bezier 曲线的扩展。B样条曲线由一系列控制点和节点向量定义，并且可以通过调整节点向量来改变曲线的形状。B样条提供了局部控制特性，即只有一部分曲线会受到单个控制点的影响，这使得它非常适合于构建复杂的形状。对于非均匀有理B样条（NURBS），它的定义如下： C(u) = \sum_{i=0}^{n} N_{i,p}(u) \frac{w_i P_i}{\sum_{j=0}^{n} N_{j,p}(u) w_j} 其中 N_{i,p}(u) 是基函数， w_i 是权重， P_i 是控制点。

  • 多段曲线的组合：C0, C1, G0, G1连续性 Composite of multiple curve segments: C0, C1,G0,G1

  • C0 连续性: 表示两段曲线在连接点处相交，但不一定有相同的切线方向。也就是说，它们的位置连续，但没有导数连续性。

  • C1 连续性: 不仅有 C0 的位置连续性，而且在连接点处具有一阶导数的连续性，这意味着它们在该点处有着相同的切线方向和斜率。

  • G0 连续性: 类似于 C0 连续性，意味着几何上两条曲线在连接点处相遇，但不考虑切线的方向。

  • G1 连续性: 几何上的一阶连续性，指在连接点处两条曲线的切线方向相同，但切线的长度可以不同。这是比 C1 更宽松的一种连续性定义，因为它只要求方向一致而不是完全相同的导数值。

Data structure and algorithms

• 数据结构 Data structure

  • 分层空间分割：四叉树、八叉树、分层包围盒、KD树、BSP树 Hierarchical spatial partition: quadtree, octree, Hierarchical bounding box, KD tree, BSP tree.
  • 如何使用数据结构组织三角网格数据 how to use data structure to organize triangular mesh data
  • 多边形裁剪、光栅化的数据结构 Data structure for polygons clipping, rasterizing
  • 光线追踪的数据结构 Data structure for ray tracing

• 算法 Algorithms

  • Cohen-Sutherland直线裁剪 Cohen-Sutherland line clipping

  Cohen-Sutherland 为每个端点定义一个 9 区域的 outcode 来快速排除那些完全位于裁剪窗口外的线段。对于每个维度，用 01、00、10 来区分 \max 的区域。

  

  • 多边形裁剪 Polygon clipping (at most one output polygon)

  多边形裁剪不同于线段裁剪，因为裁剪一个多边形可能会产生多个新的多边形。然而，裁剪凸多边形通常只会产生最多一个其他的多边形。两种常用的多边形裁剪算法是 Sutherland-Hodgman 和 Weiler-Atherton。

  • 多边形光栅化，洪泛填充 Polygon rasterizing, flood filling

  多边形光栅化（或称扫描转换）是指确定哪些像素位于由一组顶点指定的基本图元内部的过程。洪泛填充是一种递归地填充多边形内部的方法，从给定的一个种子点开始，用特定颜色替换相邻的相同颜色像素，直到遇到边界为止。

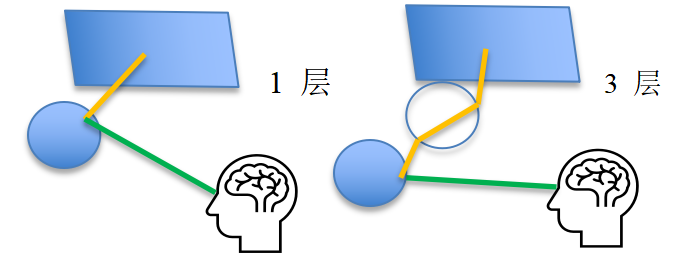
  • 光线追踪 Ray tracing

  课件给出的代码：

  trace ray
      Intersect all obiects
      color = ambient term
      For every light
          cast shadow ray
          color += local shading term
      If mirror
          color += color_refl
              trace reflected ray
      If transparent
          color += color_trans
              trace transmitted ray

  期中考试：How many levels

  

  • Z缓冲区 Z-buffer

  Z-buffer（深度缓冲区）用于解决隐藏表面移除问题。它通过存储每个像素位置处最靠近观察者的物体的深度信息，确保只有最近的物体被绘制出来。在渲染每个多边形时，比较每个像素的深度与z缓冲区中存储的深度；如果新多边形更近，则更新颜色缓冲区和z缓冲区。

Graphics related computing

• 相交 Intersection

  • 光线与平面、二次曲面 Ray and plane, quadric surface

  将光线参数化为 \mathbf r(t)=\mathbf o+t\mathbf d ，然后将其代入球体方程中，从而得到关于 t 的一元二次方程。

  • 光线与三角形、多边形、圆盘（鲁棒性） Ray and triangle, polygon, disk (robustness)

  • 光线与三角形求交的 Möller–Trumbore 算法：

    记边向量 \mathbf e_1 = \mathbf v_1 - \mathbf v_0 、 \mathbf e_2 = \mathbf v_2 - \mathbf v_0 ，辅助向量 \mathbf p_\mathbf v=\mathbf d\times \mathbf e_2 ， \text{det}=\mathbf e_1\cdot\mathbf p_\mathbf v 。若 |\text{det}|\simeq0 ，则光线几乎平行于平面，可认为无交点或在平面内。记 \text{det}^{-1}=1/\text{det} 、 \mathbf t_\mathbf v=\mathbf o-\mathbf v_0 、 \mathbf q_\mathbf v=\mathbf t_\mathbf v\times\mathbf e_1 ，检验参数 u=\text{det}^{-1}\;\mathbf t_\mathbf v\cdot\mathbf p_\mathbf v 、 v=\text{det}^{-1}\;\mathbf d\cdot\mathbf q_\mathbf v 。若 u1 则与平面无交点；若 v1 则与三角形无交点。最终可以得到 t=\text{det}^{-1}\;\mathbf e_2\cdot\mathbf q_\mathbf v ，代入 \mathbf r=\mathbf o+t\mathbf d 得到交点。

  • 多边形与圆盘：多边形可以分解为多个三角形或使用边界表示方法来进行相交测试；对于圆盘首先测试光线是否与包含圆盘的平面相交，然后检查交点是否位于圆盘的半径范围内。

• 光线与包围盒：立方体、球体、椭球体 Ray and bounding box: cube, sphere, ellipsoid

  对于由最小点 \mathbf{min} = (X_1, Y_1, Z_1) 和最大点 \mathbf{max} = (X_2, Y_2, Z_2) 定义的轴对齐边界框（AABB），对于每个维度计算交点参数 \mathbf t^{(1)}_x = (\mathbf X_1 - \mathbf o_x) / \mathbf d_x 和 \mathbf t^{(2)}_x = (\mathbf X_2 - \mathbf o_x) / \mathbf d_x （若对应分量为 0 则不参与计算），记 \text t_{s}=\max\mathbf t^{(1)} 、 \text t_e=\min \mathbf t^{(2)} ：

  • 若 0\leq\text t_s\leq\text t_e ，则存在有效交点。
  • 若 \text t_s0 ，则射线起点位于 AABB 内部。

• 加速光线与3D场景的相交：KD树、包围盒 Acceleration of ray and a 3D scene: KD tree, bounding box

  包围盒包括轴对齐边界盒（AABB）、包围球（BSphere）、任意凸区域（如OBB）等。它们被用来创建层次化的包围体积层次结构（BVH），这样可以先快速测试高层级的包围体积，如果未命中，则不必进一步考虑内部的几何体。

• 矢量 Vectors

  反射、半程矢量、法向量 Reflection, halfway, normal

  • 法向量 Normal Vector ( \mathbf{n} ) 是垂直于表面的单位向量，指向外侧，用于确定光线如何与表面相互作用，如漫反射、镜面反射等。
  • 反射矢量 Reflection Vector ( \mathbf{r} ) 当光线 \mathbf{l} 以角度 \theta 照射到一个平滑表面上时，它会按照相同的角度反射出去，也就是 \mathbf{r} = \mathbf{l} - 2(\mathbf{l} \cdot \mathbf{n})\mathbf{n} ，用于计算高光和反射路径追踪。
  • 半程矢量 Halfway Vector ( \mathbf{h} ) 位于光线 \mathbf{l} 和观察者方向 \mathbf{v} 之间的中间向量 \mathbf{h} = \frac{\mathbf{l} + \mathbf{v}}{|\mathbf{l} + \mathbf{v}|} 。用于在Phong反射模型或Blinn-Phong模型中用来近似高光位置，减少计算量而不明显牺牲精度。